Дискретная динамическая модель оптимального распределения ресурсов

 

При дискретном вложении ресурсов может возникнуть вопрос о выборе шага 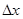 в изменении переменных управления. Этот шаг может быть задан или определяется исходя из требуемой точности вычислений и точности исходных данных. В общем случае эта задача сложна, требует интерполирования по таблицам  на предыдущих шагах вычисления. Иногда предварительный анализ уравнения состояния позволяет выбрать подходящий шаг 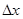, а также установить предельные значения 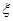, для которых на каждом шаге нужно выполнить табулирование.

Рассмотрим двумерную задачу, аналогичную предыдущей, в которой строится дискретная модель ДП процесса распределения ресурсов.

 

Задача 3. Составить оптимальный план ежегодного распределения средств между двумя предприятиями в течение трёхлетнего планового периода при следующих условиях: 1) начальная сумма составляет 400; 2) вложенные средства в размере x приносят на предприятии I доход  и возвращаются в размере 60% от x, а на предприятии II—соответственно 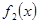 и 20%; 3) ежегодно распределяются все наличные средства, получаемые из возвращенных средств: 4) функции  и  заданы в табл. 1:

 

Таблица 1

x	50	100	150	200	250	300	350	400
	6	10	15	26	28	38	45	49
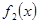
	8	12	20	28	35	40	46	48

 

Модель динамического программирования данной задачи аналогична модели, составленной в задаче 1.

Процесс управления является трехшаговым. Параметр 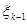 — средства, подлежащие распределению в k -м году (k =1, 2, 3). Переменная управления  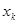— средства, вложенные в предприятие I в k -м году. Средства, вложенные в предприятие II в k -м году, составляют 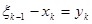.Следовательно, процесс управления на k -м шаге зависит от одного параметра  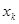(модель одномерная). Уравнение состояния запишется в виде

 

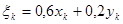,                   (2.8)

 

а функциональные уравнения – в виде

 

, (2.9)

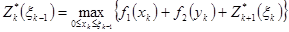.          (2.10)

 

Попытаемся определить максимально возможные значения, для которых необходимо проводить табулирование на k -м шаге (k=1, 2, 3). При 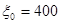 из уравнения (2.8) определяем максимально возможное значение 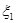; имеем  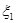=0,6-400= 2400 (все средства вкладываются в предприятие I). Аналогично, для  получаем предельное значение 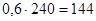. Пусть интервал изменения  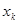совпадает с табличным, т. е. =50. Составим таблицу суммарной прибыли на данном шаге: 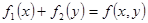(см. табл. 2). Это облегчит дальнейшие расчеты. Так как 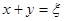, то клетки, расположенные по диагонали таблицы, отвечают одному и тому же значению , указанному в 1-й строке (в 1-м столбце) табл. 2. Во 2-й строке таблицы записаны значения , а во 2-м столбце — значения 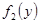, взятые из табл. 1. Значения в остальных клетках таблицы получены сложением чисел  и 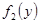. стоящих во 2-й строке и во 2-м столбце и соответствующих столбцу и строке, на пересечении которых находится данная клетка. Например, для =150 получаем ряд чисел: 20—для x =0, у =150; 18—для x =50, y ==100; 18— для x =100, y =50; 15—для x =150, y =0.

 

Таблица 2

x y	0	50	100	150	200	250	300	350	400
0	0	6	10	15	26	28	38	45	49
50	8	14	18	23	34	36	46	53
100	12	18	22	27	38	40	50
150	20	26	30	35	46	48
200	28	34	38	43	54
250	35	41	45	50
300	40	46	50
350	46	52
400	48

 

Аналогичную таблицу полезно подготовить и для расчетов по формуле (2.8). Расчет 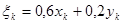 приведен в табл.3.

 

Таблица 3

x y	0	50	100	150	200	250	300	350	400
0	0	30	60	90	120	150	180	210	240
50	10	40	70	100	130	160	190	220
100	20	50	80	110	140	170	200
150	30	60	90	120	150	180
200	40	70	100	130	160
250	50	80	110	140
300	60	90	120
350	70	100
400	80

 

Проведем условную оптимизацию по обычной схеме.

3-й шаг. Основное уравнение (2.9)

 

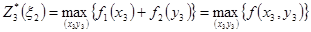
решим с помощью табл. 2. Как указывалось выше, 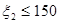. Просмотрим числа на диагоналях, соответствующих 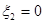; 50; 100; 150 и на каждой диагонали выберем наибольшее. Это и есть . В 1-й строке находим соответствующее условное оптимальное управление. Данные оптимизации на 3-м шаге поместим в основную таблицу (табл. 4). В ней введен столбец , который в дальнейшем используется при интерполяции.

Оптимизация 2-го шага проведена в табл. 5 согласно уравнению вида (2.10):

 

.

 

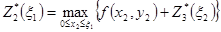Таблица 4 (основная)

	3-й шаг			2-й шаг
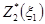
		8			10,8
50	8		50	10,8		50
		6			9,6
100	14		50	20,4		50
		6			8,0
150	20		0	28,4		100
					14
200				42,4		200
					9,2
250				51,6		200

 

Таблица 5

	50		100			150
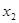
	0	50	0	50	100	0	50	100	150
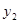
	50	0	100	50	0	150	100	50	0
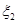
	10	30	20	40	60	30	50	70	90
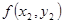
	8	6	12	14	10	20	18	18	15
	1,6	4,8	3,2	6,4	9,2	4,8	8	10,4	12,8
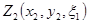
	9,6	10,8	15,2	20,4	19,2	24,8	26	28,4	27,8

Продолжение

	200					250
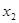
	0	50	100	150	200	0	50	100	150	200	250
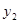
	200	150	100	50	0	250	200	150	100	50	0
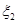
	40	60	80	100	120	50	70	90	110	130	150
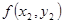
	28	26	22	23	26	35	34	30	27	31	28
	6,4	9,2	11,6	14	16,4	8	10,4	12,8	16,2	17,6	20
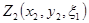
	34,4	35,2	33,6	37	42,4	43	44,4	42.8	42,2	51,6	48

 

Результаты оптимизации занесены в табл. 4. Для значений 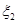, некратных 50, приведена линейная интерполяция функции  в табл. 4.

Условная оптимизация 1-го шага согласно уравнению

 

 

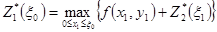
для 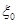=400 приведена во вспомогательной табл. 6. Для значений, некратных 50, соответствующие значения функции  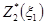получены интерполяцией в основной табл. 4.

 

Таблица 6

	0	50	100	150	200	250	300	350	400
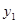
	400	350	300	250	200	150	100	50	0
	80	100	120	140	160	180	200	220	240
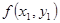
	48	52	50	50	54	48	50	53	49
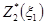
	16,6	20,4	23,6	27,8	31,2	36,8	42,4	46,1	49,8
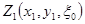
	64,6	72,4	73,6	77,8	85,2	84,8	92,4	99,1	98,8

 

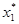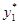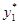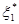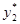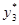Перейдем к безусловной оптимизации. Из табл. 6 получаем Z _max=99,l, =350, =50. По  и  в табл. 3 находим =220; для этого значения из табл. 4 получаем =200. Следовательно, =20. Этому управлению в табл. 3 соответствует =124; для полученного значения  из табл. 4 после интерполирования находим =24 и =100.

Итак, мы получили следующий оптимальный план распределения средств между двумя предприятиями по годам:

 

Предприятие	1-й год	2-й год	3-й год
I	350	200	24
II	50	20	100

 

При этом может быть получен максимальный доход, равный Z _max=99,l. Прямой подсчет дохода по табл. 2 для найденного оптимального управления дает 97,2. Расхождение в результатах на 1,9 (около 2%) объясняется ошибкой линейной интерполяции.

Мы рассмотрели несколько вариантов задачи оптимального распределения ресурсов. Существуют другие варианты этой задачи, особенности которых учитываются соответствующей динамической моделью.