Выразим величины 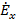 и
и  из первого и второго уравнения системы (1.3) через
из первого и второго уравнения системы (1.3) через  :
:
 (1.4)
(1.4)
Подставив их значения в последнее уравнение системы, получим дифференциальное уравнение для составляющей  :
:
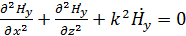 (1.5)
(1.5)
Где  .
.
Следовательно, расчет поперечно-магнитного поля в направляющей системе сводится к решению уравнения (1.5) при граничных условиях (1.1). Последние в рассматриваемом случае принимают вид
 (1.6)
(1.6)
или просто  при
при  .
.
Решение уравнения (1.5) будем искать методом разделения переменных, полагая, что
 (1.7)
(1.7)
Тогда уравнение (1.5) нетрудно привести к виду
 (1.8)
(1.8)
Последнее уравнение эквивалентно двум уравнениям:
 (1.9)
(1.9)
где  - неизвестная постоянная разделения, а
- неизвестная постоянная разделения, а
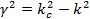 (1.10)
(1.10)
Решение первого уравнения (1.9) целесообразно записать таким образом:
 .
.
Для второго уравнения (1.9) решение удобно представить в виде линейной комбинации показательных функций:
 .
.
Следовательно,
 (
( (
( . (1.11)
. (1.11)
Чтобы найти входящие в (1.11) неизвестные коэффициенты и постоянную разделения  , используем граничные условия (1.6). Поставив туда значение
, используем граничные условия (1.6). Поставив туда значение  будем иметь
будем иметь
 (1.12)
(1.12)
при 
Условия (1.12), очевидно, могут быть удовлетворены, если положить  = 0. В этом случае проекция
= 0. В этом случае проекция  , как видно из (1.4), обращается в нуль не только на проводящих плоскостях, но и во всех точках пространства между ними. Тогда из (1.10) следует, что
, как видно из (1.4), обращается в нуль не только на проводящих плоскостях, но и во всех точках пространства между ними. Тогда из (1.10) следует, что  (величина
(величина  , как известно, носит название постоянной распространения).
, как известно, носит название постоянной распространения).
Подставляя найденные значения  и
и  в выражения (1.11) и (1.4), получим:
в выражения (1.11) и (1.4), получим:

 (1.13)
(1.13)
Здесь мы положили, что  .
.
Таким образом, решение системы уравнений (1.3) при  определяет электромагнитное поле в виде суммы двух бегущих волн, распространяющихся по оси z в противоположных направлениях.
определяет электромагнитное поле в виде суммы двух бегущих волн, распространяющихся по оси z в противоположных направлениях.
Если полагать, что источник электромагнитной энергии находится где-то в точках  , то в линии, естественно, будет существовать только одна волна, распространяющаяся в направлении от
, то в линии, естественно, будет существовать только одна волна, распространяющаяся в направлении от  к
к  . В этом случае выражения для компонент электромагнитного поля принимают вид:
. В этом случае выражения для компонент электромагнитного поля принимают вид:
 (1.14)
(1.14)
Из равенств (1.14) вытекает, что векторы электромагнитного поля полученной волны не имеют составляющих на направление распространения. Следовательно, электромагнитное поле, определяемое уравнениями (1.4), (1.5), при 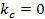 вырождается в волну поперечно-электромагнитного типа.
вырождается в волну поперечно-электромагнитного типа.
Фазовая скорость волны (1.14) совпадает со скоростью распространения плоской волны в свободном пространстве с параметрами среды  :
:

Для характеристики направляющей системы целесообразно ввести величину, называемую характеристическим сопротивлением. Последнее определяется как отношение поперечной проекции вектора 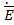 к перпендикулярной ей поперечной проекции вектора
к перпендикулярной ей поперечной проекции вектора  .
.
В нашем случае характеристическое сопротивление  будет равно
будет равно

т.е. оно совпадает с волновым сопротивлением среды для плоской волны. Такое совпадение нельзя считать случайным, ибо волна ТЕМ в рассматриваемой системе аналогична по своей структуре плоской волне в неограниченном пространстве. Действительно, если в поле плоской волны, распространяющейся в неограниченном пространстве, внести две бесконечно-тонкие проводящие плоскости, перпендикулярные вектору  , то граничные условия (1.1) автоматически оказываются выполненными.
, то граничные условия (1.1) автоматически оказываются выполненными.
Электромагнитное поле (1.14) в пространстве между проводящими плоскостями имеет волновой характер при любом значении частоты колебаний. Иными словами, поперечная волна в направляющей системе может существовать при любой частоте колебаний поля, причем распространение этой волны происходит со скоростью, зависящей лишь от параметров среды.
Полученное выше решение уравнений (1.3) оказывается не единственно возможным. В самом деле, условиям (1.6), (1.12) можно также удовлетворить если 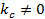 , но
, но
 при
при 
Легко убедиться, что левая часть последнего равенства будет обращаться в нуль при  , если
, если

откуда вытекает, что

Постоянная распространения  , которую в дальнейшем целесообразно обозначить
, которую в дальнейшем целесообразно обозначить  , согласно (1.10) будет равна
, согласно (1.10) будет равна
 (1.15)
(1.15)
Подставив найденное значение  в выражение (1.12) и учитывая, что
в выражение (1.12) и учитывая, что  , получим
, получим

Аналогично ранее исследованному случаю поперечной волны мы можем положить  . Тогда, в соответствии с (1.5), выражения для проекций векторов поля будут иметь вид:
. Тогда, в соответствии с (1.5), выражения для проекций векторов поля будут иметь вид:
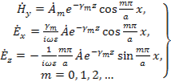 (1.16)
(1.16)
Здесь коэффициент 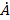 мы заменили на
мы заменили на  .
.
Так как  по определению - любое целое число, то в пространстве между параллельными проводящими плоскостями, помимо ранее найденной волны ТЕМ, может существовать бесчисленное множество полей поперечно-магнитного типа, характеризуемых различными значениями
по определению - любое целое число, то в пространстве между параллельными проводящими плоскостями, помимо ранее найденной волны ТЕМ, может существовать бесчисленное множество полей поперечно-магнитного типа, характеризуемых различными значениями  (поля
(поля 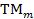 ).
).

Рис. 2 - Зависимость составляющей 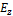 от координаты x в пространстве между проводящими плоскостями при различных значениях
от координаты x в пространстве между проводящими плоскостями при различных значениях 
Из выражений (1.16) следует, что распределение поля вдоль оси х имеет форму стоячей волны. Характер изменения поля на интервале 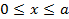 определяется числом (индексом)
определяется числом (индексом)  . Согласно (1.16) при различных
. Согласно (1.16) при различных  на промежутке между плоскостями будет укладываться различное число «полуволн» поля, причем это число как раз и равно
на промежутке между плоскостями будет укладываться различное число «полуволн» поля, причем это число как раз и равно  . На рис. 1.2 изображены кривые изменения
. На рис. 1.2 изображены кривые изменения 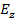 вдоль оси х, соответствующие разным
вдоль оси х, соответствующие разным  . (Максимальные значения
. (Максимальные значения  для различных «гармоник» здесь выбраны произвольно. Начальные фазы взяты или одинаковыми или отличающимися одна от другой на
для различных «гармоник» здесь выбраны произвольно. Начальные фазы взяты или одинаковыми или отличающимися одна от другой на 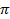 )
)
Нетрудно убедиться, что компоненты электромагнитного поля (1.16) при  совпадают с компонентами поля (1.14), ибо
совпадают с компонентами поля (1.14), ибо  соответствует
соответствует  . Следовательно, поперечно-электромагнитную волну в пространстве между параллельными проводящими плоскостями можно рассматривать как вырожденный случай поля поперечно-магнитного типа.
. Следовательно, поперечно-электромагнитную волну в пространстве между параллельными проводящими плоскостями можно рассматривать как вырожденный случай поля поперечно-магнитного типа.
Рассмотрим теперь формулу (1.15), определяющую постоянную распространения  .
.
Легко заметить, что при  ,
,  , постоянная распространения становится чисто мнимой величиной:
, постоянная распространения становится чисто мнимой величиной:
 ,
,
где

В этом случае поперечно-магнитное поле (1.16) будет иметь волновой характер, ибо выражения (1.16) при  , представляют волны, распространяющиеся с определенной скоростью вдоль оси z.
, представляют волны, распространяющиеся с определенной скоростью вдоль оси z.
Предположим, что при данных значениях частоты f, расстояния  и заданном типе поля, характеризуемом величиной
и заданном типе поля, характеризуемом величиной  , выполняется соотношение
, выполняется соотношение

В этом случае электромагнитное поле (1.16) уже не будет иметь волнового характера, так как теперь  является величиной вещественной, и множитель
является величиной вещественной, и множитель  определяет лишь экспоненциальный характер убывания амплитуды колебаний поля в различных точках оси z. Электромагнитные поля такого типа обычно называют затухающими полями (не смешивать с бегущими волнами, амплитуды которых экспоненциально затухают вдоль направления распространения).
определяет лишь экспоненциальный характер убывания амплитуды колебаний поля в различных точках оси z. Электромагнитные поля такого типа обычно называют затухающими полями (не смешивать с бегущими волнами, амплитуды которых экспоненциально затухают вдоль направления распространения).
Для любого значения  и
и  можно, очевидно, найти такую частоту колебаний, при которой постоянная распространения обращается в нуль. Из выражения (1.15) следует, что
можно, очевидно, найти такую частоту колебаний, при которой постоянная распространения обращается в нуль. Из выражения (1.15) следует, что  , если
, если

Частота колебаний электромагнитного поля, определенная из последнего равенства, имеет название критической частоты и обозначается  . Нетрудно видеть, что
. Нетрудно видеть, что
 (1.17)
(1.17)
Для каждой критической частоты можно рассчитать соответствующую ей критическую длину волны:
 ;
;  (1.18)
(1.18)
Если  и
и  , то
, то  .
.
Используя выражения (1.15), (1.17) и (1.18), получим
 (1.19)
(1.19)
Следовательно, при данных  ,
,  и
и  поперечно-магнитное поле
поперечно-магнитное поле  будет иметь форму бегущей волны в том случае, когда частота колебаний поля больше критической частоты (1.17), т. е. когда длина волны
будет иметь форму бегущей волны в том случае, когда частота колебаний поля больше критической частоты (1.17), т. е. когда длина волны  короче критической длины волны
короче критической длины волны  . Например,поле
. Например,поле  в линии с
в линии с  и
и  будет иметь волновой характер, если частота
будет иметь волновой характер, если частота  , или соответственно длина волны
, или соответственно длина волны 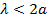 .
.
Если же частота колебаний меньше критической частоты, поле становится затухающим.
Анализируя выражения (1.16) можно показать, что перенос электромагнитной энергии вдоль направляющей системы осуществляется только бегущими волнами. В самом деле, среднее значение проекции вектора Пойнтинга на ось z в рассматриваемом случае имеет вид

Если постоянная распределения  - величина чисто мнимая, то
- величина чисто мнимая, то

При вещественном  (затухающее поле)
(затухающее поле)

Следовательно, мощность, заключенная в затухающем электромагнитном поле, является чисто колебательной. Последний вывод становится очевидным, если учесть, что проекция  в случае вещественной
в случае вещественной  сдвинута по фазе относительно проекции
сдвинута по фазе относительно проекции  на угол –
на угол –  .
.
Найдем фазовую скорость волны  . Так как по определению
. Так как по определению  , то, учитывая (1.17) - (1.18), получим
, то, учитывая (1.17) - (1.18), получим
 , (1.20)
, (1.20)
где  .
.
Отсюда вытекает, что фазовая скорость волны  при
при 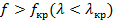 больше скорости v. При
больше скорости v. При  величина
величина  становится бесконечно большой.
становится бесконечно большой.
Характеристическое сопротивление
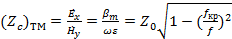 (1.21)
(1.21)
в случае поперечно-магнитных волн оказывается меньше характеристического сопротивления  .
.
Таким образом, величины, характеризующие волны TM в рассматриваемой системе, зависят и от частоты колебаний  и от расстояния а между направляющими плоскостями. Что же касается волны ТЕМ, то ее характеристики не зависят ни от
и от расстояния а между направляющими плоскостями. Что же касается волны ТЕМ, то ее характеристики не зависят ни от  , ни от
, ни от  . Получается, что направляющая система как бы не оказывает влияния на распространение этой волны.
. Получается, что направляющая система как бы не оказывает влияния на распространение этой волны.

Рис. 3 - Силовые линии векторов  и
и 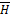 волны ТЕМ в пространстве между проводящими плоскостями
волны ТЕМ в пространстве между проводящими плоскостями
Пользуясь выражениями (1.16), можно изобразить силовые линии электромагнитного поля различных типов волн. На рис. 3 показаны силовые линии волны ТЕМ в различных координатных плоскостях (сплошные линии соответствуют электрическому полю, пунктирные - магнитному). На рис. 4 приведены силовые линии волны 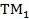 .
.

Рис. 4 - Силовые линии векторов 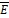 и
и 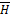 волны
волны  в пространстве между проводящими плоскостями
в пространстве между проводящими плоскостями
 2020-01-14
2020-01-14 352
352








