Скорости распространения электромагнитных волн

Пусть электромагнитная волна распространяется в среде (или направляющей системе) без потерь. В режиме установившихся гармонических колебаний мгновенные комплексные значения любой из проекций вектора 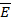 или  на оси прямоугольной системы координат имеют вид:

 

 (1.31)

 

Здесь ось z принята за направление распространения волны.

Из выражения (1.31) следует, что изменение фазы поля вдоль направления распространения определяется величиной 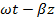. Отсюда мы находим фазовую скорость волны

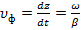 (1.32)

 

как скорость движения поверхности равных фаз вдоль оси z. Таким образом, фазовая скорость характеризует изменение начальных фаз гармонических колебаний по направлению движения волны.

Рассмотрим теперь более сложный вопрос о распространении колебаний произвольной формы. В дальнейшем такие колебания мы будем условно называть сигналами.

Очевидно, у нас нет оснований утверждать, что скорость распространения сигнала будет совпадать с фазовой скоростью. В самом деле, последняя, как было установлено, характеризует лишь фазовые соотношения между гармоническими колебаниями в различных точках пространства, когда эти колебания уже возникли и установились всюду.

Предположим, что в точке  имеется сигнал, меняющийся во времени по закону . Выясним, какой вид будет иметь этот сигнал в других точках оси z при t > 0; иными словами, определим функцию , если известна функция , а также известны характеристики среды, в которой происходит распространение. Используя интеграл Фурье, представим  в виде:

 

 (1.33)

 

где  - спектральная плотность функции . Согласно выражению (1.33) функция  представляет собой сумму множества гармонических колебаний с частотами  и амплитудами . Совокупность этих колебаний, как известно, образует спектр функции .

Но каждой составляющей  при распространении колебаний вдоль оси z соответствует волна

 

где  - волновое число. Поэтому функцию  в любой точке оси z можно представить в виде

 

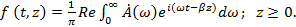 (1.34)

 

Из формулы (1.34) следует, что распространение сигнала в данном направлении обусловлено движением всех его гармонических составляющих.

В общем случае фазовая скорость волны зависит от частоты колебаний (подробнее об этом см. ниже). При наличии такой зависимости различные гармонические составляющие сигнала будут двигаться вдоль оси z с различными фазовыми скоростями. А это, очевидно, может привести к тому, что форма сигнала по мере его распространения будет изменяться.

Так как волновое число  есть функция частоты, т. е. , в (1.34) вместо интегрирования по  можно перейти к интегрированию по :

 

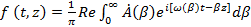. (1.35)

 

Пусть действительный спектр сигнала ограничен частотами  и , и, кроме того,  (  - средняя частота спектра). Тогда интегрирование в (1.34) будет происходить по промежутку , а в (1.35) - по промежутку . Здесь  - среднее значение волнового множителя, соответствующее средней частоте  и фазовой скорости на этой частоте, а . На основании этого вместо (1.35) будем иметь

 

 (1.36)

Сигнал, определяемый интегралом (1.36), называется волновым пакетом или группой волн.

Рассматривая  как функцию переменной , разложим  в ряд по степеням :

 

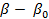 (1.37)

 

и подставим  из (1.37) в (1.36).

При малом промежутке интегрирования в разложении (1.37) можно ограничиться двумя первыми членами. В этом случае интеграл (1.36) принимает вид:

 

 

Здесь  означает производную 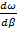 при .

Введя далее новую переменную интегрирования , получим

 

 

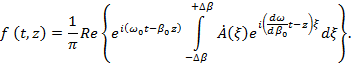
Будем полагать, что - непрерывная медленно меняющаяся функция. Тогда ее на малом интервале  можно считать постоянной, равной . В этом случае

 (1.38)

 

- аргумент комплексной величины .

Выражение (1.38), таким образом, определяет рассматриваемый сигнал в любой точке . Функция

 

 (1.39)

 

вследствие того, что  мало, является медленно меняющейся функцией переменных . Поэтому ее можно считать амплитудой волны . При 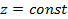 функция  является огибающей сигнала  с узким (а точнее, с бесконечно узким) частотным спектром.

Из формулы (1.39) видно, что с течением времени огибающая перемещается вдоль оси . О ее движении удобно судить по перемещению максимума, находящегося в точке .

Нетрудно сообразить, что с течением времени этот максимум движется вдоль оси  со скоростью

 

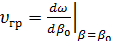 (1.40)

 

Последняя получила наименование групповой скорости. Она-то и определяет скорость распространения сигнала типа «волновой пакет».

Установим связь между групповой и фазовой скоростями. Дифференцируя выражение (1.32) по частоте, получим

 

откуда

 

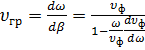 (1.41)

 

Если фазовая скорость не зависит от частоты, т.е. 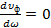, то и . В этом случае .

Зависимость фазовой скорости от частоты колебаний в физике принято называть дисперсией, а среду, в которой это явление наблюдается - дисперсной средой.

Подобная зависимость характерна, например, для нашей направляющей системы. В самом деле, фазовая скорость волны ТЕ или TM, распространяющейся между проводящими плоскостями, равна

 

 (1.42)

 

а волновое число

 

 

Используя соотношение (1.40) или (1.41), для групповой скорости получим

 

 (1.43)

и соответственно

 

 (10.44)

 

На рисунке 6 показаны графики изменения фазовой и групповой скоростей (1.42), (1.44) в зависимости от частоты колебаний.

 

Рис. 6 - Зависимость фазовой и групповой скоростей волны, распространяющейся между параллельными плоскостями, от частоты колебаний

Заключение

 

Наиболее простой направляющей системой является совокупность двух параллельных проводящих бесконечных плоскостей, пространство между которыми заполнено диэлектриком. Конечно, направляющая система такого типа представляет лишь теоретический интерес. Тем не менее, анализ электромагнитного поля в ней позволяет выяснить основные особенности распространения электромагнитных волн в реальных направляющих устройствах.

Список использованной литературы

1. Гольдштейн Л.Д., Зернов Н.В. Электромагнитные поля и волны.

2. Семенов Н.А. Техническая электродинамика.

3. Бредов М.М., Румянцев В.В., Топтыгин И.Н. Классическая электродинамика.