Означення. Два ненульових вектори  і
і  називається колінеарними, якщо відповідні їм напрямлені відрізки паралельні або лежать на одній прямій.
називається колінеарними, якщо відповідні їм напрямлені відрізки паралельні або лежать на одній прямій.
Позначення:  ||
||  (мал. 13).
(мал. 13).
Очевидно, колінеарні вектори або однаково напрямлені (мал. 13а), або протилежно напрямлені (мал. 12b). Нульовий вектор вважається колінеарним будь-якому вектору. Тому, якщо відомо, що деякі два вектори неколінеарні, то жоден з них не є нульовим вектором.
Теорема. (перша ознака колінеарності двох векторів). Два ненульових вектори  і
і  колінеарні тоді і тільки тоді, коли існує деяке число α таке, що
колінеарні тоді і тільки тоді, коли існує деяке число α таке, що  =α
=α  . /1/
. /1/
Доведення.
1. Необхідність. Нехай  ||
||  . Тоді або
. Тоді або 
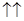
 , або
, або 

 . Якщо
. Якщо 

 , то
, то  =
= 
 , оскільки ці вектори однаково напрямлені, то вони мають однакові модулі:
, оскільки ці вектори однаково напрямлені, то вони мають однакові модулі: 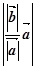 =
= 
 =
=  . Позначивши α =
. Позначивши α =  , дістанемо
, дістанемо  =α
=α  . Якщо
. Якщо 

 , то аналогічно доводиться, що
, то аналогічно доводиться, що  = -
= - 
 . Нехай α = -
. Нехай α = -  , тоді також
, тоді також  = α
= α  .
.
2. Достатність. Нехай виконується рівність /1/, тоді  і
і  або однаково, або протилежно напрямлені, а отже, вони колінеарні. Теорему доведено.
або однаково, або протилежно напрямлені, а отже, вони колінеарні. Теорему доведено.
Зауваження 1. Якщо  = 0,
= 0, 
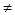 0, то теорема також справджується. У цьому випадку α =0.
0, то теорема також справджується. У цьому випадку α =0.
Зауваження 2. Оскільки для колінеарних векторів  і
і  завжди існує тільки одне число α таке, що
завжди існує тільки одне число α таке, що  = α
= α  , то звідси формально можна написати: α =
, то звідси формально можна написати: α =  , тобто можна розглядати відношення двох колінеарних векторів.
, тобто можна розглядати відношення двох колінеарних векторів.
Відношення  :
:  двох колінеарних векторів розуміють як число, на яке треба помножити вектор
двох колінеарних векторів розуміють як число, на яке треба помножити вектор  , щоб дістати вектор
, щоб дістати вектор  . Отже, відношенням двох колінеарних векторів є число, яке дорівнює відношенню їх модулів, взяте зі знаком «плюс», якщо вектори
. Отже, відношенням двох колінеарних векторів є число, яке дорівнює відношенню їх модулів, взяте зі знаком «плюс», якщо вектори  і
і  однаково напрямлені, і зі знаком «мінус», якщо вектори протилежно напрямлені.
однаково напрямлені, і зі знаком «мінус», якщо вектори протилежно напрямлені.
Компланарність векторів
Означення. Три ненульових вектори називаються компланарними
якщо відповідні їм напрямлені відрізки паралельні одній площині або лежать в одній площині.
Очевидно, що коли компланарні вектори  ,
,  ,
,  відкласти від довільної точки O (
відкласти від довільної точки O ( =
=  ,
,  =
=  ,
,  =
=  ), то точки О, А, В, С лежатимуть в одній площині (мал. 14).
), то точки О, А, В, С лежатимуть в одній площині (мал. 14).
Отже, якщо вектори компланарні, то існують такі їх представники, які лежать в одній площині.
Очевидно, що якщо серед трьох векторів є два колінеарних, то ці вектори компанарні. І навпаки, якщо три вектори некомпланарні, то серед них немає колінеарних.
Теорема 1. (про розклад вектора за двома не колінеарними векторами). Якщо вектори  ,
,  ,
,  компланарні, а вектори
компланарні, а вектори  ,
,  неколінеарні, то існують єдині числа α, βтакі, що:
неколінеарні, то існують єдині числа α, βтакі, що:  = α
= α  + β
+ β  . /2/
. /2/
Інакше кажучи, вектор  можна розкласти за векторами
можна розкласти за векторами  і
і  і до того ж єдиним способом.
і до того ж єдиним способом.
Доведення. Доведемо спочатку існування чисел α і β, що задовольняють рівність /2/. Відкладемо від деякої точки O вектори 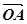 =
=  ,
,  =
=  ,
,  =
=  . Оскільки ці вектори компланарні, то точки О, А, В, С лежать в одній площині. Вектори
. Оскільки ці вектори компланарні, то точки О, А, В, С лежать в одній площині. Вектори  і
і  неколінеарні, тому O, A, B не лежать на одній прямій.
неколінеарні, тому O, A, B не лежать на одній прямій.
Можливі два випадки:
1. Точка С належить прямій ОВ (мал. 15a). Тоді вектори  і
і  колінеарні і, отже, за попередньою теоремою,
колінеарні і, отже, за попередньою теоремою,  = β
= β  , де β – деяке число. Отже,
, де β – деяке число. Отже,  =0*
=0*  + β
+ β  , тобто має місце розклад /2/.
, тобто має місце розклад /2/.
2. С  (ОВ). Проведемо
(ОВ). Проведемо  || OB (мал. 15b). Тоді за правилом трикутника
|| OB (мал. 15b). Тоді за правилом трикутника  =
=  +
+  . Але ця рівність можлива тільки тоді, коли α =
. Але ця рівність можлива тільки тоді, коли α =  , β =
, β =  . Дійсно, якби, наприклад, α
. Дійсно, якби, наприклад, α 
 , то було б,
, то було б, 
 ||
||  , що суперечить умові теореми. Отже, припущення неправильне. Тому існує єдиний розклад вектора
, що суперечить умові теореми. Отже, припущення неправильне. Тому існує єдиний розклад вектора  за векторами
за векторами 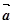 і
і  . Теорему доведено.
. Теорему доведено.
Теорема 2. ( про розклад вектора за трьома некомпланарними векторами). Якщо вектори 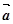 ,
,  ,
,  некомпланарні, то для будь-якого вектора
некомпланарні, то для будь-якого вектора  , існують і притому єдині числа α, β, γ такі, що
, існують і притому єдині числа α, β, γ такі, що  = α
= α 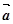 +β
+β  +γ
+γ  .
.
 2020-01-14
2020-01-14 333
333








