Множення вектора на число

 

Означення. Добутком вектора  на дійсне число α називається вектор 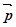, який задовольняє такі умови:

1) = * ;

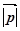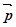
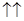
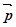
2) , якщо α >0, і , якщо α <0.

Такий вектор позначається 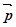= α .

Операція добутку вектора на число має такі властивості.

Властивість 1. α* =0* =  для будь-якого дійсного числа α і будь-якого вектора . Ця властивість випливає з умови 1) означення.

Властивість 2. Для будь-якого вектора  1* = ; -1* =- . Ця властивість випливає безпосередньо з означення.

Властивість 3. Для будь-якого вектора  і будь-яких дійсних чисел α і β: α(β )=(αβ) .

Доведення. Нехай α(β )= 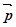, (αβ) = . Доведемо, щ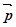о = . Маємо:

= * = * * ,

= * = * * .

 

 

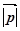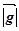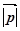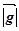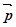
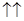
Отже, = . Покажемо, що . Якщо α і β одного знаку, то вектор 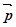 однаково напрямлений з  і  однаково напрямлений з .Отже, 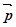. У випадку коли числа α і β протилежних знаків, 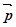, . Отже, також , що й треба було довести.

 

Властивість 4. Операція множення вектора на число дистрибутивна відносно додавання векторів, тобто α( + )=α +α , для ,  і α  R.

Доведення. Нехай α > 0. Відкладемо вектори = , = , =α , =α  (мал. 11). Тоді + = , α +α = . Покажемо, що =α . Оскільки вектори  і α ,  і α  відповідно однаково напрямлені, то відповідні кути A і  у трикутників OAB і  рівні (як кути утворені при перетині двох паралельних прямих третьою). Крім того, сторони цих трикутників, що прилягають до рівних кутів, пропорційні: . Тому OAB ~ . Звідси випливає, що OAB= , а це означає, що промені OB і 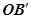 збігаються, тобто . 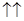Крім того =α* = * . Тому =α* .

 

 

Аналогічно розглядається випадок, коли α <0 (мал. 12).

Випадок α = 0 тривіальний. Отже, α ( + ) = α +α .

 

Властивість 5. Операція множення вектора на число дистрибутивна відносно додавання чисел, тобто (α+β) =α +β ,  і α, β R.

Доведення. Розглянемо два можливих випадки: αβ >0 і αβ <0 (випадок αβ=0 не викликає труднощів).

1. Нехай αβ >0, тобто числа α і β одного знаку. Тоді вектори (α+β)  і α +β  однаково напрямлені. Крім того,

;

.

Отже,  і вектори (α+β)  та α +β  рівні.

2. Нехай αβ <0, тобто числа α і β різних знаків. Якщо α = -β, то (α+β) =(-β+β) =0 =0; α +β = -β + β =0, отже, властивість справджується.

Якщо α 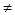-β, тоді –α, α+β або –β, α+β одного знаку. Нехай, наприклад, -α, α+β одного знаку. Тоді за доведеним (-α) + (α+β) =(-α+α+β) =β (α+β) = α +β , що і треба було довести.