Содержание
Введение…………………………………………………………………………...3
Глава I. Определение обратных тригонометрических функций.
1.1. Функция у = arcsin x ……………………………………………………........4
1.2. Функция у = arccos x …………………………………………………….......5
1.3. Функция у = arctg x ………………………………………………………….6
1.4. Функция у = arcctg x …………………………………………………….......7
Глава II. Решение уравнений с обратными тригонометрическими функциями.
2.1. Основные соотношения для обратных тригонометрических функций….8
2.2. Решение уравнений, содержащих обратные тригонометрические функции……………………………………………………………………..11
2.3. Вычисление значений обратных тригонометрических функций…..........21
Заключение……………………………………………………………………….25
Список использованной литературы…………………………………………...26
Введение
Во многих задачах встречается необходимость находить не только значения тригонометрических функций по данному углу, но и, обратно, угол или дугу по заданному значению какой-нибудь тригонометрической функции.
Задачи с обратными тригонометрическими функциями содержатся в заданиях ЕГЭ (особенно много в части В и С). Например, в части В Единого государственного экзамена требовалось по значению синуса (косинуса) найти соответствующее значение тангенса или вычислить значение выражения, содержащего табличные значения обратных тригонометрических функций. Относительно этого типа заданий заметим, что таких заданий в школьных учебниках недостаточно для формирования прочного навыка их выполнения.
Т.о. целью курсовой работы является рассмотреть обратные тригонометрические функции и их свойства, и научиться решат задачи с обратными тригонометрическими функциями.
Чтобы достичь цели, нам потребуется решить следующие задачи:
· Изучить теоретические основы обратных тригонометрических функций,
· Показать применение теоретических знаний на практике.
Глава I. Определение обратных тригонометрических функций
1.1. Функция у = arcsin x
Рассмотрим функцию  ,
,  .
.  (1)
(1)
В этом промежутке функция  монотонна (возрастает от -1 до 1), следовательно, существует обратная функция
монотонна (возрастает от -1 до 1), следовательно, существует обратная функция
 ,
,  . (2)
. (2)
Каждому данному значению у (величины синуса) из промежутка [-1,1] соответствует одно вполне определенное значение х (величины дуги) из промежутка  . Переходя к общепринятым обозначениям, получаем
. Переходя к общепринятым обозначениям, получаем
 , где
, где  . (3)
. (3)
Это и есть аналитическое задание функции, обратной функции (1). Функция (3) называется арксинусом аргумента  . График этой функции – кривая, симметричная графику функции
. График этой функции – кривая, симметричная графику функции  , где
, где  , относительно биссектрисы I и III координатных углов.
, относительно биссектрисы I и III координатных углов.
Приведем свойства функции  , где
, где  .
.
Свойство 1. Область изменения значений функции  :
:  .
.
Свойство 2. Функция  – нечетная, т.е.
– нечетная, т.е. 
Свойство 3. Функция  , где
, где  , имеет единственный корень
, имеет единственный корень  .
.
Свойство 4. Если  , то
, то 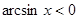 ; если
; если  <x
<x  , то
, то  .
.
Свойство 5. Функция  монотонна: при возрастании аргумента
монотонна: при возрастании аргумента  от -1 до 1 значение функции возрастает от
от -1 до 1 значение функции возрастает от  до
до  .
.

1.2. Функция y = arсcos x
Рассмотрим функцию  ,
,  . (4)
. (4)
В этом промежутке функция  монотонна (убывает от +1 до -1), значит, для нее существует обратная функция
монотонна (убывает от +1 до -1), значит, для нее существует обратная функция
 ,
,  , (5)
, (5)
т.е. каждому значению  (величины косинуса) из промежутка [-1,1] соответствует одно вполне определенное значение
(величины косинуса) из промежутка [-1,1] соответствует одно вполне определенное значение  (величины дуги) из промежутка [0,
(величины дуги) из промежутка [0,  ]. Переходя к общепринятым обозначениям, получаем
]. Переходя к общепринятым обозначениям, получаем
 ,
,  . (6)
. (6)
Это и есть аналитическое задание функции, обратной функции (4). Функция (6) называется арккосинусом аргумента х. График этой функции можно построить на основании свойств графиков взаимно обратных функций.
Функция  , где
, где  , обладает следующими свойствами.
, обладает следующими свойствами.
Свойство 1. Область изменения значений функции  :
:  .
.
Свойство 2. Величины 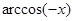 и
и  связаны соотношением
связаны соотношением
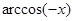 =
= 
 .
.
Свойство 3. Функция  имеет единственный корень
имеет единственный корень  .
.
Свойство 4. Функция  отрицательных значений не принимает.
отрицательных значений не принимает.
Свойство 5. Функция  монотонна: при возрастании аргумента
монотонна: при возрастании аргумента  от -1 до +1 значения функции убывают от
от -1 до +1 значения функции убывают от  до 0.
до 0.

1.3. Функция y = arctgx
Рассмотрим функцию  ,
, 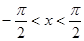 . (7)
. (7)
Отметим, что эта функция определена для всех значений  , лежащих строго внутри промежутка от
, лежащих строго внутри промежутка от  до
до  ; на концах этого промежутка она не существует, так как значения
; на концах этого промежутка она не существует, так как значения 
 - точки разрыва тангенса.
- точки разрыва тангенса.
В промежутке  функция
функция  монотонна (возрастает от -
монотонна (возрастает от -  до
до  ), следовательно, для функции (1) существует обратная функция:
), следовательно, для функции (1) существует обратная функция:
 ,
, 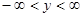 , (8)
, (8)
т.е. каждому данному значению  (величины тангенса) из промежутка
(величины тангенса) из промежутка  соответствует одно вполне определенное значение
соответствует одно вполне определенное значение  (величины дуги) из промежутка
(величины дуги) из промежутка  .
.
Переходя к общепринятым обозначениям, получаем
 ,
,  . (9)
. (9)
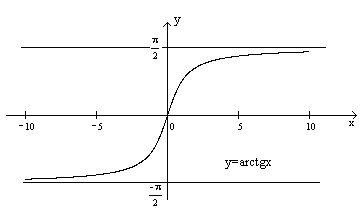
Это и есть аналитическое задание функции, обратной (7). Функция (9) называется арктангенсом аргумента х. Отметим, что при 
 значение функции
значение функции 
 , а при
, а при 


 , т.е. график функции имеет две асимптоты:
, т.е. график функции имеет две асимптоты: 
 и
и 
 .
.
Функция  ,
,  , обладает следующими свойствами.
, обладает следующими свойствами.
Свойство 1. Область изменения значений функции  .
.
Свойство 2. Функция  – нечетная, т.е.
– нечетная, т.е.  .
.
Свойство 3. Функция  имеет единственный корень
имеет единственный корень  .
.
Свойство 4. Если  , то
, то 
 ; если
; если 

 , то
, то 
 .
.
Свойство 5. Функция  монотонна: при возрастании аргумента от
монотонна: при возрастании аргумента от 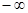 до
до  значения функции возрастают от
значения функции возрастают от  до +
до +  .
.
1.4. Функция y = arcctgx
Рассмотрим функцию  ,
, 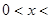
 . (10)
. (10)
Эта функция определена для всех значений 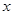 , лежащих внутри промежутка от 0 до
, лежащих внутри промежутка от 0 до  ; на концах этого промежутка она не существует, поскольку значения
; на концах этого промежутка она не существует, поскольку значения  и
и 
 - точки разрыва котангенса. В промежутке (0,
- точки разрыва котангенса. В промежутке (0,  ) функция
) функция  монотонна (убывает от
монотонна (убывает от  до
до 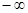 ), следовательно, для функции (1) существует обратная функция
), следовательно, для функции (1) существует обратная функция
 ,
,  , (11)
, (11)
т.е. каждому данному значению  (величины котангенса) из промежутка (
(величины котангенса) из промежутка ( ) соответствует одно вполне определенное значение
) соответствует одно вполне определенное значение 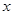 (величины дуги) из промежутка (0,
(величины дуги) из промежутка (0,  ). Переходя к общепринятым обозначениям, получаем
). Переходя к общепринятым обозначениям, получаем
 ,
, 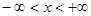 . (12)
. (12)
Это и есть аналитическое задание функции, обратной (10). Функция (12) называется арккотангенсом аргумента 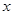 .
.
График функции имеет две асимптоты: 
 и
и  .
.
Функция  ,
, 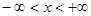 , обладает следующими свойствами.
, обладает следующими свойствами.
Свойство 1. Область изменения значений функции:  .
.
Свойство 2. Величины  и
и 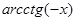 связаны соотношением
связаны соотношением  .
.
Свойство 3. Функция  корней не имеет.
корней не имеет.
Свойство 4. Функция  отрицательных значений не принимает.
отрицательных значений не принимает.
Свойство 5. Функция  монотонна: при возрастании
монотонна: при возрастании 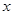 от
от  до
до  значения функции убывают от
значения функции убывают от  до 0.
до 0.

 2020-01-14
2020-01-14 233
233







