Традиционные способы решения уравнений с обратными тригонометрическими функциями (аркфункциями) сводятся к вычислению какой-нибудь тригонометрической функции от обеих частей с последующим преобразованием полученных суперпозиций по известным тригонометрическим формулам и формулам приведенных ниже:






 (13)
(13)



Формулы (13) легко выводятся из определений аркфункций и основных тригонометрических тождеств. Приведенные формулы можно дополнить подобными им формулами, полученными на основе двух тождеств
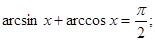 (14)
(14)

и формул приведения.
Основным недостатком упомянутых способов решения является нарушение равносильности уравнения в процессе его преобразования, вследствие чего можно ожидать появления “лишних” корней. Выявление лишних решений путем подстановки в исходное уравнение зачастую вызывает большие трудности либо а) из-за сложности вычислений не табличных значений аркфункций, либо б) в связи с тем, что полученное множество решений бесконечно.
Существует метод решения уравнения с аркфункциями, в процессе которого “лишние” корни вообще не возникают. Метод реализуется в трех приводимых ниже подходах, которые различаются в зависимости от числа аркфункций, участвующих в уравнении.
Подход(I): Исходное уравнение содержит две аркфункции. Разнесем их в разные части уравнения. Зададим двумя неравенствами области изменения левой и правой части уравнения. Ввиду монотонности аркфункций эти неравенства легко разрешаются относительно аргументов указанных функций. Решение последней системы неравенств и определяет тот промежуток, которому принадлежат корни исходного уравнения.
Задача 1. Решить уравнение

Решение: Для сравнения воспользуемся сначала традиционной схемой решения.
ОДЗ: 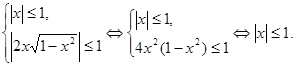
Далее,
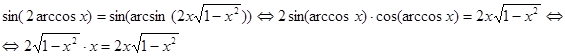
С учетом ОДЗ, 
В полученном интервале содержится бесконечное множество “лишних” решений, удаление которых превращается здесь в отдельную задачу.
Альтернативное решение, использующее метод (I):
Положим  Так как
Так как  и
и  то исходное уравнение равносильно следующей системе:
то исходное уравнение равносильно следующей системе:


Ответ: 
Задача 2. Решить уравнение

Решение: Положим  Перепишем уравнение в виде:
Перепишем уравнение в виде:

Так как  то исходное уравнение равносильно системе:
то исходное уравнение равносильно системе:



Ответ: 
Задача 3. Решить уравнение

Решение: Обозначим
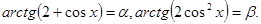
Так как  и
и  то
то  и
и 
Уравнение принимает вид  причем
причем
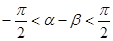 и
и 
Так как 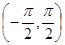 - интервал монотонности тангенса, то уравнение
- интервал монотонности тангенса, то уравнение  равносильно уравнению
равносильно уравнению 
Переходя к уравнению

можно потерять те корни, для которых  и
и  не существует. В данном случае этого не произойдет, поскольку
не существует. В данном случае этого не произойдет, поскольку

А правые части существуют всегда. Получаем уравнение

которое после преобразований принимает вид
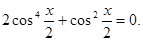
Так как уравнение  не имеет решений, то остается
не имеет решений, то остается 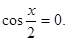
Ответ: 
Подход (II): Пусть исходное уравнение содержит более двух аркфункций. В этом случае равносильность преобразований сохраняется при использовании следующих схем решения:
(II.1) 
(II.2) 
При решении задач проверка неравенств  или
или  не вызывает сложностей и сводится к сопоставлению областей изменения входящих в уравнение аркфункций.
не вызывает сложностей и сводится к сопоставлению областей изменения входящих в уравнение аркфункций.
Задача 4. Решить уравнение: 
Решение: Положим  Исходное уравнение равносильно системе:
Исходное уравнение равносильно системе:

Так как  то достаточно убедиться, что
то достаточно убедиться, что 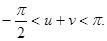
Правое неравенство верно в силу границ изменения арктангенса. Левая часть неравенства следует из того, что  при
при 
Ответ: 
Задача 5. Решить уравнение: 
Решение: Положим  Тогда исходное уравнение равносильно системе:
Тогда исходное уравнение равносильно системе: 
 (*)
(*)
Последнее неравенство с очевидностью следует из неравенств  задающих промежутки изменения переменных. Поэтому система (*) равносильна следующей системе:
задающих промежутки изменения переменных. Поэтому система (*) равносильна следующей системе: 
Корень первого уравнения системы  является решением исходного уравнения. После сокращения первого уравнения на
является решением исходного уравнения. После сокращения первого уравнения на  возводим его в квадрат.
возводим его в квадрат.

Так как 
То 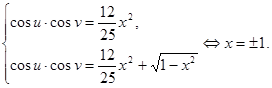
Ответ: 
Задача 6. Решить уравнение 
Решение: Пусть

Так как  то обе части уравнения лежат в интервале монотонности синуса. Поэтому уравнение равносильно такому:
то обе части уравнения лежат в интервале монотонности синуса. Поэтому уравнение равносильно такому:

или

После упрощений получим уравнение

имеющее единственный корень  Делаем проверку и убеждаемся, что
Делаем проверку и убеждаемся, что  является корнем предыдущего уравнения и, следовательно, корнем исходного уравнения.
является корнем предыдущего уравнения и, следовательно, корнем исходного уравнения.
Ответ: 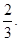
Задача 7. Решить уравнение

Решение: Введем обозначения

Данное уравнение принимает вид 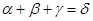 или
или 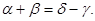 Обе части уравнения лежат в интервале
Обе части уравнения лежат в интервале  Если взять котангенсы от обеих частей уравнения, то можно потерять лишь корень, которому соответствует значение углов, равное 0, так как это – единственное значение из интервала
Если взять котангенсы от обеих частей уравнения, то можно потерять лишь корень, которому соответствует значение углов, равное 0, так как это – единственное значение из интервала  в котором котангенс не существует. Проверим, будет ли выполняться равенство
в котором котангенс не существует. Проверим, будет ли выполняться равенство  Если
Если  то
то  откуда
откуда  и
и  При
При  получаем, что
получаем, что  Таким образом,
Таким образом,  - корень уравнения.
- корень уравнения.
Если  то от обеих частей уравнения можно взять котангенсы:
то от обеих частей уравнения можно взять котангенсы:

Что приведет к следствию исходного уравнения. Раскрыв скобки и подставив выражения тригонометрических функций  и
и 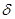 через
через  получим уравнение
получим уравнение

которое равносильно системе
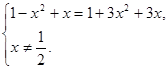
Получаем два значения неизвестного:  Проверкой убеждаемся, что оба значения удовлетворяют данному уравнению.
Проверкой убеждаемся, что оба значения удовлетворяют данному уравнению.
Подход (III): Для упрощения исходного уравнения во многих случаях удобно переходить от одних аркфункций к другим (например, от арксинуса или арккосинуса к арктангенсу). При этом, наряду с формулами (14), можно использовать следующие формулы:

 (15)
(15)



Задача 8. Решить уравнение:

Решение: Заметим, что  не удовлетворяет данному уравнению. Поэтому, в силу формул (15),
не удовлетворяет данному уравнению. Поэтому, в силу формул (15),


Итак, исходное уравнение можно записать в виде:

Если  то уравнение принимает вид:
то уравнение принимает вид:
 что невозможно.
что невозможно.
Если 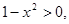 то и в этом случае уравнение
то и в этом случае уравнение
 решений не имеет, поскольку
решений не имеет, поскольку
 для
для 
Ответ: нет решений.
Задача 9. Решить уравнение 
Решение: 
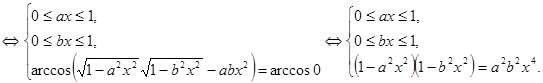
Из полученной системы следует, что  то есть
то есть  и
и  - числа одного знака. Действительно, если
- числа одного знака. Действительно, если  то
то  и
и 
Если же 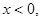 то из неравенств сразу следует, что
то из неравенств сразу следует, что  и
и  Следовательно, если
Следовательно, если  то уравнение решений не имеет.
то уравнение решений не имеет.
Если  то уравнение также решений не имеет, так как
то уравнение также решений не имеет, так как
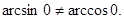
Пусть  и хотя бы одно из чисел не равно нулю. Тогда получим, что
и хотя бы одно из чисел не равно нулю. Тогда получим, что
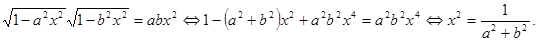
Учитывая ограничения системы, получаем, что если  и хотя бы одно из чисел не равно нулю, то
и хотя бы одно из чисел не равно нулю, то 
Если же  и хотя бы одно из чисел не равно нулю, то
и хотя бы одно из чисел не равно нулю, то 
Ответ: если  то уравнение решений не имеет; если
то уравнение решений не имеет; если 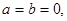 то уравнение решений не имеет; если
то уравнение решений не имеет; если  и хотя бы одно из чисел не равно нулю, то
и хотя бы одно из чисел не равно нулю, то  если
если  и хотя бы одно из чисел не равно нулю, то
и хотя бы одно из чисел не равно нулю, то 
Задача 10. Решить систему уравнений 
Решение: Используя формулы группы 2, получим:


Обращаясь к методам алгебраических систем уравнений, получим, что  и
и  являются корнями квадратного уравнения
являются корнями квадратного уравнения

Получим

Ответ: 
 2020-01-14
2020-01-14 1399
1399
