Основные соотношения
Приведем 6 групп формул, которые могут значительно облегчить решение задач, содержащих основные тригонометрические функции:
1. 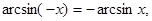
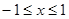 ;
;
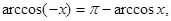
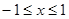 ;
;
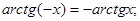

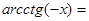
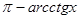 .
.
Формулы данной группы наиболее часто используются при решении тригонометрических уравнений.
2. 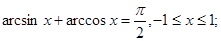
Вывод: По определению 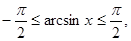
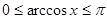 и
и 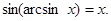
Заметим, что 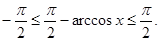 По формуле приведения имеем
По формуле приведения имеем
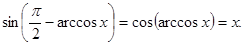
 Итак, аргументы
Итак, аргументы 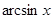 и
и 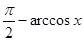 заключены в отрезке
заключены в отрезке 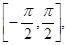 в котором синус монотонно возрастает от -1 до +1, и имеют одинаковый синус, равный
в котором синус монотонно возрастает от -1 до +1, и имеют одинаковый синус, равный 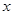 . Следовательно, сами аргументы также равны, т.е.
. Следовательно, сами аргументы также равны, т.е. 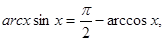 откуда и получаем тождество
откуда и получаем тождество 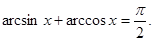


3. 
Вывод: Пусть 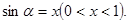 Тогда
Тогда
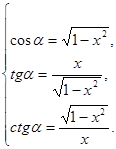 (1’)
(1’)
Равенство (1’) вместе с исходным равенством равносильны следующим равенствам:
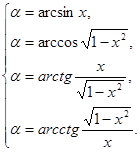 (2’)
(2’)
Эти равенства вытекают из самого определения обратных тригонометрических функций.
Так как левые части всех равенств (2’) равны между собой, то равны и их правые части. 

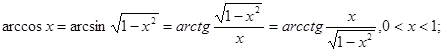
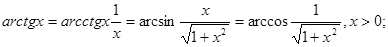

4. 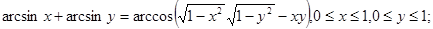
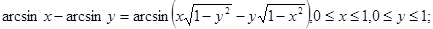
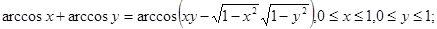
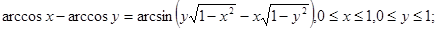
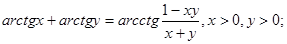
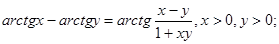
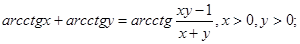
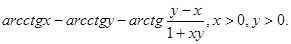
5. 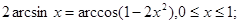
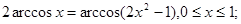
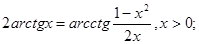
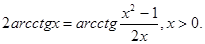
6. 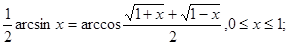
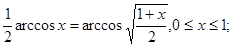
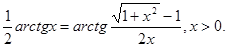
 2020-01-14
2020-01-14 234
234








