Методы решения однородных линейных систем дифференциальных уравнений

1 2 3 4 5 6

1) Сведение к одному уравнению n-ого порядка. (Этот метод мы разбирали выше)

2) Решение ЛОСДУ с постоянными коэффициентами с помощью матриц (видоизмененный метод Эйлера).

Пусть дана система n линейных дифференциальных уравнений с n неизвестными функциями, коэффициенты которой постоянные:

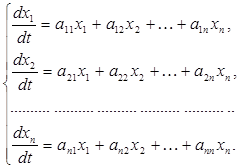(11)

Эту систему можно записать в виде одного матричного дифференциального уравнения

Здесь

[2 стр 169]

Ищем решение системы в виде:

X₁=α₁e^kt, X₂=α₂e^kt,…….X_n=α_ne^kt.(12)

Требуется определить постоянные α_1, α₂,…, α_n и k так, чтобы функции α₁e^kt, α₂e^kt,…,α_ne^kt удовлетворяли системе уравнений (11). Подставим их в систему(1), получим:

Сократим на e^kt. Перенося все члены в одну сторону и собирая коэффициенты при α_1, α₂,…., α_n, получим систему уравнений

Выберем α_1, α₂,…., α_n и k такими, чтобы удовлетворялась система (13).Эта система есть система линейных однородных алгебраических уравнений относительно α_1, α₂,…., α_n. Составим определитель системы (13):

(14)

Если k таково, что определитель ∆ отличен от нуля, то система (13) имеет только нулевые решения α₁=α₂=…=α_n=0,а следовательно, формулы (12) дают только тривиальные решения:

X₁(t)=X₂(t)=…=X(t)=0.

Таким образом, нетривиальные решения (12) мы получим только при таких k,при которых определитель (14) обращается в нуль. Мы приходим к уравнению n-ого порядка для определения k:

(15)

Это уравнение называется характеристическим уравнением для системы (1),его корни называются корнями характеристического уравнения.

Рассмотрим несколько случаев.

Случай 1. Корни характеристического уравнения действительны и различны. Обозначим через k₁, k₂,….k_n корни характеристического уравнения. Для каждого корня k_j напишем систему (13) и определим коэффициенты

α₁⁽ⁱ⁾,α₂⁽ⁱ⁾,…, α_n⁽ⁱ⁾.

Можно показать, что один из них произвольный, его можно считать равным единице. Таким образом, получаем:

для корня k₁решение системы (11)

Для корня k₂ решение системы (1)

……………………………………………………….

для корней k_n решение системы (1)

Путем непосредственной подстановки в уравнения можно убедиться, что система функций

(16)

где С₁, С₂,….,С_n -произвольные постоянные, тоже является решением системы дифференциальных уравнений (11). Это есть общее решение системы (11). Легко показать, что можно найти такие значения постоянных, при которых решение будет удовлетворять заданным начальным условиям.

Случай 2. Корни характеристического уравнения различные, но среди них есть комплексные. Пусть среди корней характеристического уравнения имеется два комплексных сопряженных корня:

k₁ = α+iβ, k₂= α-iβ.

Этим корням будут соответствовать решения

(j = 1, 2, …,n), (17)

(j = 1, 2, …,n), (18)

Коэффициенты α _j⁽¹⁾ иα _j⁽²⁾определяются из системы уравнений (13).

Можно показать, что действительные и мнимые части комплексного решения тоже являются решениями. Таким образом, мы получаем два частных решения:

(19)

Где - действительные числа, определяемые через и . Соответствующие комбинации функций (18) войдут в общее решение системы. [2 стр 112-115]

Случай 3. Характеристическое уравнение имеет единственный корень k (кратности 2), которому соответствуют два линейно независимых собственных вектора P₁и P₂(т.е. кратность корня совпадает с числом линейно независимых собственных векторов). Векторы P₁и P₂ порождают два линейно независимых решения

И общее решение, так же как и в случае 1, находится по формуле (4).

Случай 4. Характеристическое уравнение имеет единственный корень k (кратности 2), которому с точностью до постоянного множителя соответствует один собственный вектор P₁(т.е. кратность корня больше числа линейно независимых собственных векторов). В этом случае для отыскания решения целесообразно применить метод неопределенных коэффициентов. Согласно этому методу общее решение необходимо искать в форме

Где постоянные С_ij требуют определения путем подстановки этих выражений в исходную однородную систему.

Замечание. Для решения однородных систем в случае, когда корень характеристического уравнения λ кратный и ему соответствует единственный собственный вектор P₁, может быть применен метод присоединения векторов.

Суть его такова. Пусть P₂– вектор-столбец, являющийся решением уравнения

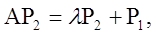(20)

тогда однородная система

(21)

имеет два линейно независимых решения

Покажем, что Y₂ является решением. Имеем

Учитывая, что P₁ и - собственный вектор, а P₂удовлетворяет условию (20), получаем

Нетрудно также убедиться, что Y₁ и Y₂ линейно независимы. Следовательно, они образуют фундаментальный набор решений, и общее решение может быть найдено по формуле (4).

В общем случае корню характеристического уравнения λ кратности k>1, имеющему один собственный вектор P₁,соответствует k линейно независимых решений