Введение
Дифференциальные уравнения.
Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции.
Дифференциальное уравнение первого порядка.
Рассмотрим вопросы теории дифференциальных уравнений на примере уравнений первого порядка, разрешенных относительно производной, т.е. таких, которые допускают представление в виде
 (1.1)
(1.1)
где f - некоторая функция нескольких переменных.
Теорема существования и единственности решения дифференциального уравнения. Пусть в дифференциальном уравнении (1.1) функция  и ее частная производная
и ее частная производная  непрерывны на открытом множестве Г координатной плоскости Оху. Тогда:
непрерывны на открытом множестве Г координатной плоскости Оху. Тогда:
.Для всякой точки  множества Г найдется решение y=y(x) уравнения(1.1),удовлетворяющее условию
множества Г найдется решение y=y(x) уравнения(1.1),удовлетворяющее условию  y(
y( 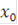 );
);
2.Если два решения y=  (x) и y=
(x) и y=  (x) уравнения (1.1) совпадают хотя бы для одного значения x=
(x) уравнения (1.1) совпадают хотя бы для одного значения x= 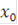 , т.е. если
, т.е. если 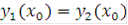 то эти решения совпадают для всех тех значений переменной х, для которых они определены. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде
то эти решения совпадают для всех тех значений переменной х, для которых они определены. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде
 g(y) (1.2)
g(y) (1.2)
или в виде
M(x)N(y)dx+P(x)Q(y)dy=0, (1.3)
где  , M(x), P(x) - некоторые функции переменной х, g(y), N(y), Q(y) - функции переменной у.
, M(x), P(x) - некоторые функции переменной х, g(y), N(y), Q(y) - функции переменной у.
 (рис.1)
(рис.1)
Дифференциальные уравнения с разделяющимися переменными
Для решения такого уравнения его следует преобразовать к виду, в котором дифференциал и функции переменной х окажутся в одной части равенства, а переменной у - в другой. Затем проинтегрировать обе части полученного равенства. Например из (1.2) следует, что  =
=  и
и  =
=  . Выполняя интегрирование, приходим к решению уравнения (1.2)
. Выполняя интегрирование, приходим к решению уравнения (1.2)
Пример 1. Решить уравнение  dx=xydy.
dx=xydy.
Решение. Разделив левую и правую части уравнения на выражение х 
(при х ≠0), приходим к равенству  . Интегрируя, получим
. Интегрируя, получим
 (a)
(a)
или
 +
+  , (б)
, (б)
(так как интеграл в левой части (а) табличный, а интеграл в правой части может быть найден, например, заменой  = t,
= t,  , 2ydy=2tdt и
, 2ydy=2tdt и 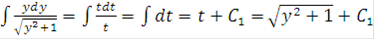 .
.
Решение (б) перепишем в виде x=±  или x=C
или x=C  , где C=±
, где C=±  .
.
 2020-04-20
2020-04-20 203
203







