Методические рекомендации к оформлению контрольных работ

По переходным процессам

Оформление пояснительной записки.

Пояснительную записку следует оформлять как текстовый документ в соответствии с ГОСТ 2.105 - 95. Она должна содержать титульный лист и текстовую часть с расчетами и электрическими схемами.

Выполняется пояснительная записка на стандартных листах белой бумаги формата А4 с рамкой на каждом листе. На первом листе записки выполняют основную надпись по форме 2, а на последующих – в правом нижнем углу листа ставится порядковый номер страницы. В тексте следует применять научно-технические термины, обозначения и определения, установленные стандартами, а при их отсутствии – общепринятые в научно-технической литературе.

Значения и разъяснения символов и числовых коэффициентов, входящих в формулы, должны быть приведены непосредственно под формулой, и первая строка расшифровки должна начинаться со слов,,где'' без двоеточия после него. Расчеты, выполняемые по формулам, должны включать формулу с буквенными обозначениями, а затем с подстановкой вместо буквенного обозначения числовых значений, используемых в расчете величин. Если величины используются в именованных единицах (Ом, А и т.д.), то именованные значения можно ставить только у конечного значения, полученного по расчетной формуле. Если величины используются в относительных единицах, то размерности не проставляются.

Схемы должны выполняться в соответствии с требованиями ЕСКД. Все графики и характеристики должны выполняться в координатной сетке в масштабе.

П р и л о ж е н и е П2

Комплексные числа в теории электрических цепей

Переменного тока

1. Форма представления:

A – комплексное число (вектор на комплексной плоскости).

А = а + jв = Ae^jα = A(cosα + jsinα);

A = a – jв = Ae^-jα = A(cosα – jsinα);

A = - модуль комплексного числа;

α = arctg 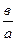- аргумент комплексного числа;

j = - мнимая единица;

а – вещественная часть комплексного числа;

в – коэффициент при мнимой части комплексного числа (мнимая часть);

Специальные обозначения:

α = Arg(A); a = Re(A); в = Im(A).

Формула Эйлера (доказывается разложением в ряд):

Изображение комплексного числа на координатной плоскости (на комплексной плоскости) (рис. 1-П2).

Рис. 1-П2

А ₁ = а₁ + jв₁ = =A₁cosα₁ + jA₁sinα₁;

a₁ = A₁cosα₁;

в₁ = А₁sinα₁.

2. Простейшие математические операции.

Комплексное число может не иметь вещественной или мнимой части:

1 = 1 + j0; -5 = -5 + j0;

j = 0 + j1; -j = 0 – j1.

Умножение и деление на чисто мнимое число j:

- умножение на +j равнозначно повороту вектора, изображающего комплексное число на комплексной плоскости, на 90⁰ в положительном направлении (против хода часовой стрелки) (рис. 1 – П2, рис. 3 – П2)

Рис. 2-П2

А = А ^.j =

(т.е. умножение вещественного числа А на j переводит вещественное число в чисто мнимое jA).

Рис. 3-П2

;

- деление на +j равнозначно умножению на –j, то есть повороту вектора на угол 90⁰ в отрицательном направлении, так как

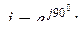
3. Понятие оператора поворота.

- оператор поворота вектора А на угол 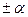, если вектор А умножается на . При этом модуль вектора остается неизменным. Здесь (.

4. Операции над комплексными числами.

Операции умножения и деления проще выполнять, если комплексные числа представлены в показательной форме:

A ^. B = A e ^jαB e ^jβ = AB e ^j(α+β);

Операции сложения и вычитания проще выполнять, если комплексные числа представлены в алгебраической форме:

A = a₁ + ja₂; A + B = (a₁ + в₁) + j(a₂ + в₂);

В = в₁ + jв₂; А – В = (а₁ – в₁) + j(a₂ – в₂).

5. Понятие сопряженного комплексного числа.

Комплексное число Â называется сопряженным по отношению к комплексному числу А, если у последнего изменить знак перед мнимой частью на противоположный:

Â = а – jв, если А = а + jв;

Â = а + jв, если А = а - jв;

Â = , если А = Ае ^jα, и т. п.

6. Умножение на е ^А:

А = а + jв; B = c + jd.

B · е ^А = B · е^{а +}^j^в = B · е^а + е^j^в.

Здесь е^а – вещественное число, е^jв – оператор поворота на угол в.

Таким образом, вектор В увеличивается по модулю в е^а раз и поворачивается затем на угол в, представленный в радианах, см. курс высшей математики.

За единицу измерения угла принимается радиан – угол в 1 рад равен 57,3⁰. Это угол, при котором длина дуги равна радиусу. Так угол 90⁰ соответствует рад, 180⁰ π рад и т.д.

7. Оператор поворота а.

Поворот вектора на угол 120⁰ осуществляется умножением его на оператор поворота е^j¹²⁰. В электротехнике этот оператор обозначают буквой а. На рис. 4 -П2

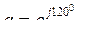
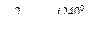тогда

Рис. 4-П2

8. Выражения оператора поворота,, а'' в различной форме:

a = е^j ¹²⁰ = -0,5 + j 0,87; a ² = e^j ²⁴⁰ = -0,5 – j 0,87;

-a = 0,5 – j 0,87 = e^-j ⁶⁰; a ³ = 1;

a ² + a = -1; a ² + a + 1= 0;

a ² – a = e^-^j ⁹⁰ = 0 - j ; a – a ² = e^j ⁹⁰ = 0 + j ;

1 – a = e^-^j ³⁰ = 1,5 – j 0,87; 1 – a ² = e^j ³⁰ = 1,5 + j 0,87.

9. Представление комплексного сопротивления (рис. 5-П2).

Z = R + jX; (X_L > 0; X_C < 0);

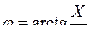
(в данном случае на рис. 5-П2 Х = Х_L > 0).

Рис. 5-П2

10. Комплексные параметры электрической цепи переменного тока.

Рис. 6-П2

комплекс тока;

комплексное сопротивление.

По закону Ома комплексное напряжение на участке цепи 1 – 2 (рис.6-П2)

U ₁₂ = I ^. Z = I ^.Z

Отставание тока от напряжения равно разности аргументов:

ψ_u – ψ_i = (ψ_i + φ) – ψ_i = φ.

Комплексная мощность

S = U ₁₂ ^. Î = U₁₂ ^.

= U₁₂ ^.I(cosφ + jsinφ) = P₁₂ + jQ₁₂.

Синусоидальные величины могут быть получены как проекции вращающихся векторов, например (рис. 7–П2):

a = A ^. sinα = A ^. sinωt,

где α = ωt – угловое положение вектора, вращающегося со скоростью ω.

Рис. 7-П2

Если к началу времени наблюдения процесса t = 0 синусоидальная величина имела значение А ₀ = А ^. sin α ₀, то запись дальнейшего синусоидального процесса во времени имеет вид

a = A sin(ωt + α ₀).

Стадия изменения синусоидальной величины, характеризуемая изменением во времени t текущего значения угла (α₀ + ωt), называется фазой синусоидального процесса, α₀ – начальная фаза.

Вектор, вращающийся в положительном направлении, то есть против часовой стрелки, с угловой скоростью ω может быть выражен следующим образом:

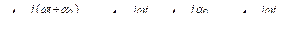
где А = А∟α₀ – комплексная амплитуда, представляющая данный вектор в момент t = 0. Иначе говоря, это комплексная величина, не зависящая от времени, модуль и аргумент которой равны соответственно амплитуде и начальной фазе заданной синусоидальной функции.

Если синусоидальная функция имеет одну и ту же частоту, то соответствующие этим функциям векторы вращаются с одинаковой угловой скоростью ω = 2πf, и поэтому углы между ними сохраняются неизменными (f – частота в Гц).

На рис. 8-П2,а показаны две синусоидальные функции

u ₁ = U ₁ _m sin(ωt + ψ ₁) и u ₂ = U ₂ _m sin(ωt – ψ ₂),

имеющие одинаковую угловую частоту ω. Функция и ₁опережает по фазе функцию и ₂,причем фазовый сдвиг равен разности начальных фаз:

Этот угол образуют между собой векторы (комплексы напряжений), показанные на рис. 8-П2,б.

Рис. 8-П2

Диаграмма, изображающая совокупность векторов, построенная с соблюдением их взаимной ориентации по фазе, называется векторной диаграммой.

Векторное представление синусоидальных функций, частота которых одинакова, облегчает операции сложения и вычитания этих функций. Например, если двум синусоидальным функциям соответствуют комплексные амплитуды А и В, то сумме этих синусоидальных функций соответствует комплексная амплитуда С = А + В.

10. Законы Ома и Кирхгофа в комплексной форме.

Рис. 9 -П2

Пусть к последовательной цепи элементов R, L, C (рис. 9-П2) приложено напряжение u = Im(U _me^jωt) = U _m sinωt = U_m sin(ωt + ψ). В цепи будет протекать синусоидальный ток той же частоты

I = I_m sin(ωt + ψ – φ).

Пусть заданное синусоидальное напряжение символизируется комплексной функцией U _me^jωt, а искомый синусоидальный ток – комплексной функцией I _me^jωt; комплексные амплитуды напряжения и тока равны соответственно

U _m = U_m ^.e ^j^ψ; I _m = I_m ^.e ^j(^ψ^-^φ⁾.

Уравнение Кирхгофа для цепи рис. 9 -П2

u = R ^. i + L

запишем через мнимые части соответствующих комплексов

Операции над мнимыми частями комплексных функций могут быть заменены операциями над самими комплексными функциями с последующим выделением мнимой части полученного результата. Следовательно, последующая запись будет иметь вид

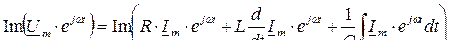Полученные уравнения справедливы для любого момента времени, поэтому заключенные в скобки комплексные выражения, от которых берется мнимая часть, должны быть равны друг другу. Производя с ними операции дифференцирования и интегрирования, получаем