Допустим, что к цепи с параллельным соединением резистора, катушки и конденсатора (рис. 3.7) приложено синусоидальное напряжение
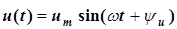 .
.
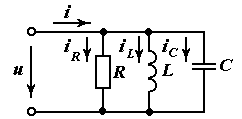
Рис. 3.7. Электрическая цепь с параллельным включением
резистора, катушки и конденсатора
Это напряжение приложено к каждому из параллельно включенных элементов и вызывает в них токи
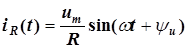 ,
,
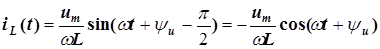 ,
,
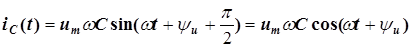 .
.
| И 3.40 | Определение 1. Составляющая синусоидального тока, фаза которой равна фазе напряжения, называется активной составляющей. Составляющая тока, фаза которой больше или меньше фазы напряжения на 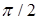 , называется реактивной составляющей. , называется реактивной составляющей. |
| И 3.41 | Определение 2. Активная составляющая входного тока двухполюсника пропорциональна напряжению на нем; коэффициент пропорциональности  называют эквивалентной активной проводимостью двухполюсника. называют эквивалентной активной проводимостью двухполюсника. |
Комментарий к определению 2. В рассматриваемой цепи (рис. 3.7) активная проводимость двухполюсника
обратно пропорциональна активному сопротивлению резистора. В более сложной цепи активная проводимость может зависеть от сопротивлений всех элементов, составляющих эту цепь.
| И 3.42 | Определение 3. Амплитуда реактивной составляющей тока пропорциональна амплитуде приложенного напряжения; коэффициент пропорциональности 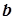 называется эквивалентной реактивной проводимостью двухполюсника. называется эквивалентной реактивной проводимостью двухполюсника. |
Комментарий к определению 3. В рассматриваемой цепи (рис. 3.7) реактивная проводимость двухполюсника равна
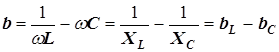 ,
,
здесь величина 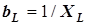 - это индуктивная проводимость идеальной катушки;
- это индуктивная проводимость идеальной катушки; 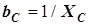 - емкостная проводимость конденсатора. Реактивная проводимость двухполюсника в рассматриваемом примере
- емкостная проводимость конденсатора. Реактивная проводимость двухполюсника в рассматриваемом примере
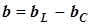 ,
,
она является алгебраической величиной. В более сложных цепях эквивалентная реактивная проводимость может зависеть от сопротивлений всех элементов, включая резисторы.
Итак, входной ток любого линейного двухполюсника можно разложить на активную и реактивную составляющие
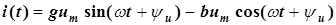 . (3.25)
. (3.25)
Для этого нужно знать его активную и реактивную проводимости.
Полная проводимость
Входной ток и входное напряжение двухполюсника в цепи переменного сисинусоидального тока связаны формулой (3.25). Преобразуем линейную комбинацию синусоиды и косинусоиды в синусоиду с некоторой начальной фазой по формулам (3.18) и (3.19):
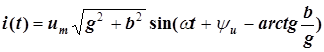 . (3.26)
. (3.26)
Амплитуда тока равна
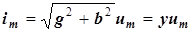 ,
,
соответственно действующие значения тока и напряжения связаны равенством
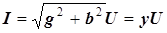 . (3.27)
. (3.27)
| И 3.43 | Определение. Коэффициент пропорциональности между действующими значениями (или амплитудами) входного тока и напряжения на двухполюснике 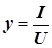 (3.28) называется полной проводимостью двухполюсника. (3.28) называется полной проводимостью двухполюсника. |
| И 3.44 | Полная проводимость двухполюсника равна геометрической сумме активной и реактивной проводимостей: 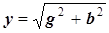 . (3.29) . (3.29) |
Определение полной проводимости (3.28) и одно из ее важнейших свойств (29) сформулированы на основании равенств (3.27).
| И 3.45 | Полная проводимость является величиной, обратной полному сопротивлению: 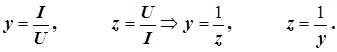 (3.30) (3.30) |
Предостережение. Активная проводимость, как правило, не является величиной, обратной активному сопротивлению двухполюсника. Только для некоторых простых двухполюсников выполняется соотношение 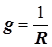 . Аналогично, реактивная проводимость в общем случае не является величиной, обратно пропорциональной реактивному сопротивлению двухполюсника. Только для некоторых простых двухполюсников выполняется условие
. Аналогично, реактивная проводимость в общем случае не является величиной, обратно пропорциональной реактивному сопротивлению двухполюсника. Только для некоторых простых двухполюсников выполняется условие 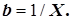
 2020-04-07
2020-04-07 2802
2802
