Действовать без правил – самое трудное и самое утомительное занятие на этом свете.
А. Мандзони
ГЛАВА 2. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Объединение, пересечение и разность множеств, симметрическая разность множеств, дополнение множества, законы и тождества алгебры множеств, доказательство тождеств с множествами, метод двух включений, метод доказательства от противного, диаграммы Эйлера – Венна
ЦЕЛИ
Освоив эту главу, студенты должны:
· знать основные свойства операций над множествами;
· уметь выполнять операции над множествами;
· уметь доказывать тождества с множествами.
2.1. Объединение множеств
Объединением множеств А и В называют множество С, которое состоит из тех элементов, которые принадлежат или множеству А, или множеству В, или обоим множествам одновременно:
С = А È В,
где È — знак объединения.
Теоретико-множественная запись операции объединения имеет следующий вид:
x ÎC = A È B ® x ÎA Ú x ÎB,
что означает: элемент х принадлежит множеству С, если х принадлежит множеству А или множеству В. Если изобразить элементы множеств А и В точками плоскости, расположенными внутри прямоугольника, то A È B представится множеством точек плоскости, расположенных внутри заштрихованной фигуры (рис.2.1). Такое геометрическое представление множеств называется диаграммой Эйлера-Венна.
Также можно записать: элемент х не принадлежит множеству С, если он не принадлежит множеству A и не принадлежит множеству В:
xÏC = A È B ® xÏA & xÏB.
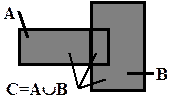
Рис. 2.1. Пример операции объединения множеств А и В
Например, найдем объединение множеств А = { ЭВМ, студент } и В = { 1, 2, стол, ЭВМ, стул }. Результатом будет множество С = А È В = { 1, 2,стол, ЭВМ, стул, студент }.
Приведем основные свойства операции объединения:
· A È A = A - идемпотентность;
· A È B = B È A - коммутативность;
· (A È B) È C = A È (B È C) - ассоциативность;
· A È Æ = A;
· (A Í A È B) & (B Í A È B).
Объединение в множествах является синонимом сложения в арифметике.
Заметим, что можно объединить не только два, но и любое количество множеств.
Объединением n множеств А1, А2,..., А n называется множество, обозначаемое: 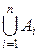 , состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств A i:
, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств A i:
А1 È А2 È А3 È … А n = 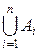 .
.
Мощность объединения множеств равна числу содержащихся в нем неповторяющихся элементов. Например, А = {1, 2, 3}, B = {1, 2, 9, 10}, C = А È В = {1, 2, 3, 9, 10} и мощность |C| = 5.
2.2. Пересечение множеств
Множество С называется пересечением множеств А и В, если оно состоит из тех элементов, которые принадлежат одновременно множеству А и множеству В:
С = А Ç В,
где Ç — знак пересечения.
На рис.2.2. приведена диаграмма Эйлера-Венна, иллюстрирующая пересечение множеств А и В. Множество A Ç B изображено заштрихованной фигурой.
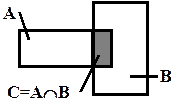
Рис. 2.2. Пример операции пересечения множеств
Теоретико-множественная запись операции пересечения имеет следующий вид:
x ÎC = A Ç B ® x ÎA & x ÎB,
что означает: элемент х принадлежит множеству С, если х одновременно принадлежит множеству А и множеству В.
Соответственно элемент х не принадлежит множеству С, если он не принадлежит множеству А или не принадлежит множеству В:
x ÏC = A Ç B ® x ÏA Ú x ÏB.
Приведем пример пересечения множеств A = { 1, 2, 3 } и B = { 3, 4, 5, 6 }. Результатом выполнения данной операции будет множество C = A Ç B = { 3 }.
Свойства операции пересечения:
· A Ç A = А - идемпотентность;
· A Ç B = B Ç A - коммутативность;
· (A Ç B) Ç C = A Ç (B Ç C) - ассоциативноcть;
· A Ç Æ = Æ;
· A Ç B =А «А Í B;
· A Ç B Í А & A Ç B Í B.
Пример, когда пересечение двух множеств равняется пустому множеству, показан с помощью диаграммы Эйлера-Венна на рис. 2.3.
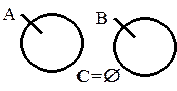
Рис. 2.3. Пример операции пересечения
Отметим, что операция пересечения может выполняться над любым количеством множеств. Пересечением n множеств А1, А2,..., Аn называется множество, обозначаемое через 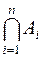 , состоящее из тех и только тех элементов, которые принадлежат каждому из множеств:
, состоящее из тех и только тех элементов, которые принадлежат каждому из множеств:
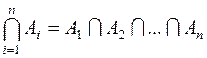 .
.
Примеры пересечения трех и четырех множеств на основе диаграмм Эйлера-Венна показаны на рис. 2.4, 2.5.
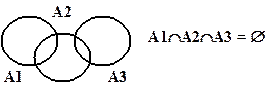
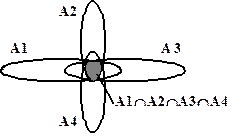
Рис. 2.4. Пример пересечения Рис. 2.5. Пример пересечения
трех множеств четырех множеств
Например, пересечением множеств А = {1, 2, 3}, B = {1, 2, 9, 10} является множество C = {1, 2} и его мощность |C| = 2.
2.3. Разность множеств
В отличие от первых двух операций операция разности применима только к двум множествам.
Множество С называется разностью множеств А и В, если С состоит из тех элементов, которые одновременно принадлежат множеству А и не принадлежат множеству В:
С = А \ В,
где \ — знак разности.
Теоретико-множественная запись операции разности имеет следующий вид:
x ÎC = A \ B ® x ÎA & x ÏB,
что означает: элемент х принадлежит множеству С, если х принадлежит А и одновременно х не принадлежит множеству В.
Соответственно элемент х не принадлежит множеству С, если он не принадлежит множеству А или принадлежит множеству В:
x ÏC = A \ B ® x ÏA Ú x ÎB.
Например, заданы множества A = {1, 2} и B = {3, 8, 9}. Тогда разность между множествами A и B равна A \ B = {1, 2}, а разность между множествами B и A равна B \ A = {3, 8, 9}.
На рис. 2.6 приведены диаграммы Эйлера-Венна, иллюстрирующие операцию разности множеств A\B, а также разности множеств B \ A.
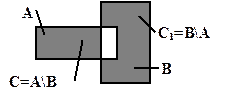
Рис. 2.6. Пример операции разности множеств
Очевидно, что:
А \ А = Æ; А \ U = Æ; В \ Æ = В; Æ \ А = Æ.
Основные свойства операции разности множеств:
· (A \ B) \ C = A \ (B \ C) = (A \ C) \ B - ассоциативноcть;
· A \ B Í A, B \ A Í A.
Множество С называется симметрической разностью множеств А и В, если С состоит из тех элементов и только тех элементов универсального множества U, которые принадлежат множеству А и не принадлежат множеству Вилипринадлежат множеству В и не принадлежат множеству А:
С = А Å В,
где Å — знак симметрической разности.
Теоретико-множественная запись операции симметрической разности имеет следующий вид:
x ÎC = A Å B ® (x ÎA & x ÏB) Ú (x ÎВ & x ÏА).
Например, заданы множества A = { 1, 2, 3, 8 } и B = { 3, 4, 8, 9 }. Тогда симметрическая разность A и B равна A Å B = { 1, 2, 4, 9 }.
2.4. Дополнение множества
Множество 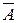 называется дополнением множестваА до некоторого универсального множества U, если оно состоит из элементов, принадлежащих множеству U и не принадлежащих множеству А. Теоретико-множественная запись операции дополнения имеет вид
называется дополнением множестваА до некоторого универсального множества U, если оно состоит из элементов, принадлежащих множеству U и не принадлежащих множеству А. Теоретико-множественная запись операции дополнения имеет вид
x Î 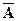 = U \ A ® x ÎU & x ÏA,
= U \ A ® x ÎU & x ÏA,
x Ï 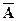 = U \ A ® x ÏU Ú x ÎA.
= U \ A ® x ÏU Ú x ÎA.
На рис. 2.7 приведена диаграмма Эйлера-Венна, иллюстрирующая операцию дополнения множества А. Множество точек, расположенных в заштрихованной фигуре, образует множество 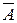 .
.

Рис. 2.7. Пример дополнения множества А до универсального множества U
Основные свойства операции дополнения множества:
· 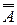 = A,
= A,
· A È 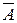 = U,
= U,
· A Ç 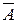 = Æ,
= Æ,
· 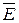 = Æ,
= Æ,
· 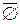 = U.
= U.
2.5. Тождества алгебры множеств
Применяя операции объединения и пересечения, разности и дополнения к множествам, можно составить из множеств алгебраические выражения.
Если два или несколько алгебраических выражений над одними и теми же множествами представляют одно и то же множество, то эти выражения можно приравнять друг к другу, получив алгебраическое тождество.
Основные тождества алгебры множеств:
Пусть А, В и С - произвольные подмножества семейства Â(U).
· 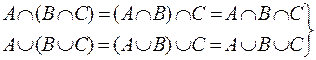 - ассоциативность;
- ассоциативность;
· 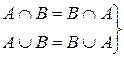 - коммутативность;
- коммутативность;
· 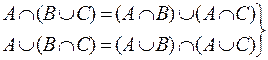 - дистрибутивность;
- дистрибутивность;
· 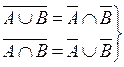 - закон Де Моргана;
- закон Де Моргана;
· 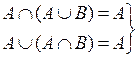 - закон поглощения;
- закон поглощения;
· 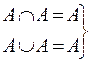 - закон тавтологии;
- закон тавтологии;
· 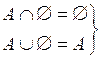 ;
;
· A \ B = A \ (A Ç B);
· A \ B = A Ç 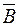 ;
;
· A \ (A \ B) = A Ç B;
· A Ç (B \ C) = (A Ç B) \ (A Ç C).
Приведем формулу включений-исключений, которая позволяет вычислять мощности объединения двух множеств:
|A È B| = |A| + |B| - |A Ç B|.
Например, заданы множества A = { 1, 2, 3, 8 } и B = { 3, 4, 5, 8, 9 }. Тогда |A| = 4, |B| = 5, |A Ç B| = 2, |A È B| = 4 + 5 – 2 = 7.
2.6. Доказательства тождеств с множествами
Введем понятие записи. Например, выражение A Ç (B \ C) является записью. Число букв и знаков операций является длиной записи. В приведенном примере длина записи равна 5. Отметим, что различные по длине записи могут соответствовать одним и тем же множествам. Например, запись A Ç (B \ C) и запись(A Ç B) \ (A Ç C) равны, хотя имеют разную длину (5 и 7).
При построении логических устройств необходимо использовать записи минимальной длины. Для их нахождения используются доказательства тождеств с множествами.
Рассмотрим способы доказательства равенств с множествами. Равенство с множествами имеет две формы:
1) E(A, B, C...) = F(A, B, C...).
E и F — высказывания над множествами A, B, C и т.д. Необходимо доказать или опровергнуть, что они равны.
2) E(A, B, C...) = Æ.
Доказать или опровергнуть, что высказывание равно Æ.
Рассмотрим методы доказательства тождеств с множествами. Здесь используется метод двух включений (взаимного включения), который основан на свойстве включения множеств:
E = F ® EÍF & FÍE.
Причем доказательство включения E Í F называется необходимостью, а доказательство включения F Í E - достаточностью.
Например, необходимо доказать или опровергнуть справедливость тождества (A È B) Ç C = (A Ç C) È (B Ç C). Левую часть тождества обозначим Е, а правую F. Тогда нам необходимо доказать или опровергнуть, что
E Í F & F Í E.
1. Докажем необходимость: E Í F.
Для доказательства этой части предполагается, что существует какой-то элемент, принадлежащий множеству E, и далее путем различных преобразований делается попытка доказать, что этот элемент принадлежит F.
a Î E ® a Î[(A È B) Ç C] ® a Î (A È B) & a Î C ® (a Î A Ú a Î B) & a Î C ® a Î (A Ç B) & a Î (B Ç C) ® a Î [(A Ç C) È (B Ç C)] ® a Î F.
Следовательно, мы доказали, что Е включается в F.
2. Докажем теперь достаточность, т.е. докажем, что если a Î F, то a Î E.
a Î F ® a Î [(A Ç C) È (B Ç C)] ® a Î (A Ç C) Ú a Î (B Ç C) ® a Î A & a Î C Ú a Î B & a Î C ® a Î (A È B) & a Î C ® a Î [(A È B) Ç C] ® a Î E.
Следовательно, мы доказали, что F включается в E.
Значит, E = F и исходное тождество справедливо.
Для доказательства тождеств с множествами, записанными во второй форме, используется метод от противного. Например, докажем справедливость тождества
A \ [(A Ç B) È (A \ B)] = Æ.
Метод от противного предполагает, что это выражение не равно Æ, т.е. существует какой-то элемент, принадлежащий этому выражению. Здесь пытаются найти противоречие.
Обозначим левую часть тождества через Е и будем считать, что она не равна пустому множеству. Тогда существует хотя бы одни элемент, принадлежащий Е:
E ¹ Æ ® a Î E ® a Î A & a Ï [(A Ç B) È (A \ B)] ® a Î A & (a Ï (A Ç B) & a Ï (A \ B)) ® a Î A & (a Ï A & a Ï B) & (a Ï A Ú a Î B).
Таким образом, мы получили противоречие, когда элемент а одновременно принадлежит и не принадлежит множеству А. Значит, наше первоначальное предположение неверно и исходное тождество справедливо, т.е. равно Æ.
Для множеств небольшого размера используют геометрический метод доказательства тождеств, основанный на использовании диаграмм Эйлера-Венна. Для доказательства тождества геометрическим методом необходимо построить диаграммы Эйлера-Венна для анализируемых записей. На одной из них выделить точки плоскости, представляющие множество левой части тождества, а на другой выделить точки плоскости, представляющие множество правой части тождества. Если фигуры на обеих диаграммах одинаковы, то тождество справедливо.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 2.1. Пусть A = {1, 3, 5, 7, 9} и B = {3, 5, 6, 10, 11}. Множества А и В являются элементами семейства Â(N), где N - множество натуральных чисел. Найти A È B, A Ç B, А \ В, 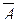 .
.
Ответ: A È B = {1, 3, 5, 7, 9, 10, 11, 6}; A Ç B = {3, 5}; A \ B = {1, 7, 9}; 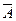 = {2, 4, 6, 8, 10, 11, 12,...}.(Множество Nв данной задаче является универсумом).
= {2, 4, 6, 8, 10, 11, 12,...}.(Множество Nв данной задаче является универсумом).
Пример 2.2. Пусть A = { x ÎN | х - четнoe число}, В = { x | ($ y)(y ÎN & x = 2 y +1}, C = { x | ($ y)(y ÎN & x = 4 y }.
Найти A È B, A Ç B, А \ В, A È C, A \ C.
Решение: Множества А, В, С являются подмножествами множества N. Множество В состоит из нечетных натуральных чисел, а множество А - из четных натуральных чисел, следовательно, A Ç B = Æ, A È B = N, A \ B = A. Элементы множества С - натуральные числа, кратные четырем, следовательно, множество С является собственным подмножеством множества А, а A È C = A,A \ C = { x Î N | ($ y)(y Î N & x = 4 y + 2)}.
Ответ: A È B = N, A Ç B = Æ, A \ B = A, A È C = A, A \ C = { x Î N | ($ y)(y Î N & x = 4 y + 2)}.
Пример 2.3. Докажите, что для записи последовательности операций объединения и пересечения необходимы круглые скобки, если количество операций больше одной.
Решение: Пусть имеется последовательность операций над произвольными множествами А, В, С - A Ç B È C, которую можно рассматривать как A Ç (B È C) либо как (A Ç B) È C. Покажем, что последние два множества не равны.
Предположим, что A = Æ, а C ¹ Æ.
Тогда (A Ç B) È C = (Æ Ç B) È C = Æ È C = C, в то время, как A Ç (B È C) = Æ Ç (B È C) = Æ.
Ответ: Таким образом, доказано, что (A Ç B) È C¹A Ç (B È C).
Пример 2.4. Доказать, что A Í B ® 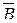 Í
Í 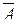 .
.
Решение: Пусть А и В - подмножества некоторого универсума Е и А Í В, тогда справедлива следующая последовательность утверждений:
(" x Î E)(x Î A ® x Î B); (" x Î E)(x Ï B ® x Ï A); (" x Î E)(x Î 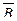 ® x Î
® x Î 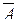 ),значит
),значит 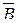 Í
Í 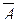 .
.
Ответ: Мы доказали, что A Í B влечет, что 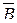 Í
Í 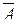 .
.
Пример 2.5. Доказать, используя метод взаимного включения, закон дистрибутивности пересечения относительно объединения:
A Ç (B È C) = (A Ç B) È (A Ç C).
Для доказательства этого тождества необходимо доказать, чтоA Ç (B È C) Í (A Ç B) È (A Ç C), a затем что(A Ç B) È (A Ç C) Í A Ç (B È C).Докажем первое включение, показывая истинность последовательности импликаций.
1. Необходимость.
(" x Î Е)(x Î (A Ç (B È C)) ® x Î A & (x Î B Ú x Î C) ®
(импликация истинна на основе определения операций объединения и пересечения)
x Î A & x Î B Ú x Î A & x Î C ® x Î (A Ç B) Ú x Î (A Ç C) ®
(использован дистрибутивный закон)
x Î ((A Ç B) È (A Ç C)) ® A Ç (B È C) Í (A Ç B) È (A Ç C).
(использовано определение включения в высказывательной форме)
Таким образом, доказано прямое включение множеств (необходимость).
2. Достаточность. Теперь докажем обратное включение:
(" x Î Е)(x Î ((A Ç B) È (A Ç C))) ® x Î (A È B) Ú x Î (A È C) ®
x Î A & x Î B Ú x Î A & x Î C ®
x Î A & (x Î B Ú x Î C) ®
x Î A & x Î B È C ® x Î (A Ç (B È C)) ®
(A Ç B) È (A Ç C) Í A Ç (B È C).
Обратное включение также доказано.
Ответ: Таким образом, дистрибутивность пересечения относительно объединения доказана.
Пример 2.6. Доказать, используя геометрический метод, закон дистрибутивности объединения относительно пересечения:
A È (B Ç C) = (A È B) Ç (A È C).
Для доказательства заданного тождества отметим на диаграмме рис. 2.8,а множество точек, соответствующих множеству A È (B Ç C),а на диаграмме рис. 2.8,б - множество точек, соответствующих множеству (A È B) Ç (A È C).
На рис. 2.8,а светлой штриховкой отмечено множество В Ç С, а серой штриховкой - множество А, множество A È (B Ç C) на диаграмме представлено фигурой, представляющей собой объединение фигур, заштрихованных вышеуказанным образом.
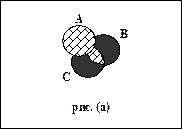
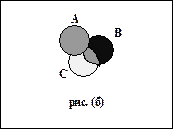
Рис. 2.8. Пример диаграммы Эйлера-Венна
На рис. 2.8,б множество A заштриховано серым, множество B - черным, а множествоC - белым цветом, тогда объединение множеств A È Bпредставляет собой фигуру, объединяющую серый и черный круги, объединение множеств A È C – фигуру, объединяющую серый и белый круги, а пересечение множеств A È Bи A È C представлено множеством A и множеством точек внутри фигуры, имеющей одинаковую с множеством A штриховку.
Ответ: Сравнивая эти два рисунка, можно сделать вывод, что эти множества равны, следовательно, тождество доказано.
Пример 2.7. Доказать, используя метод от противного, истинность тождества:
A Ç (B \ A) = Æ.
Решение: Предположим, что A Ç (B \ A) ¹ Æ, т.е. существует элемент х, принадлежащий множеству, стоящему в левой части тождества. Покажем с помощью последовательных импликаций, что наше предположение ложно:
($ x)(x Î (A Ç (B \ A)) ® x Î A & x Î (B \ A) ®
x Î A & (x Î B & x Ï A) ® x Î A & x Î B & x Ï A ®Æ & x Î B ® Æ
(использовано свойство коммутативности)
Ответ: Таким образом, исходное тождество доказано.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое взаимное включение множеств и в каком случае существует взаимное включение?
2. Что называется объединением, пересечением, разностью и дополнением множеств?
3. В каком случае объединение, пересечение и разность двух множеств равны пустому множеству?
4. Как определяется симметрическая разность множеств?
5. Привести примеры множеств:
а) объединение которых равно их пересечению;
б) пересечение множеств равно Æ, а их разность не является пустым множеством.
6. Приведите основные тождества алгебры множеств.
7. Поясните операцию дополнения множеств.
8. Какие методы доказательства тождеств с множествами вам известны?
9. Что представляет из себя метод доказательства тождеств с множествами от противного?
10. На чем основан метод взаимного включения?
11. На чем основан геометрический метод доказательства тождеств с множествами?
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Пусть множества А, В и С являются подмножествами множества S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 3, 4, 5, 10}, B = {2, 4, 7, 8, 9}, C = {5, 8, 10}.
Найти: A È B, A \ C, 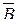 Ç (A È C).
Ç (A È C).
2. Пусть A = { x | x - женское имя}; B = {Мария, Иван, Петр, Иванов}; C = { x | x - фамилия}.
Найти: A Ç B, A Ç C, B Ç C.
3. Показать, что для записи последовательности операций объединения и разности необходимы круглые скобки.
4. Показать на диаграммах Эйлера-Венна справедливость утверждения задания 3.
5. Доказать, что B Í A & C Í A Þ B È C Í A.
6. Выполнить разбиения множества В на 5 классов: B = { a, b, c, 1, 2, 3}.
7. Для произвольных множеств А, В, С Î Â(E) доказать или опровергнуть следующие тождества методом включения множеств.
а) A È (B Ç C) = (A È B) Ç (A È C);
б) 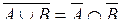 ;
;
в) 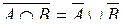 ;
;
г) A \ B = A \ (A Ç B);
д) A \ B = A Ç 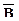 ;
;
е) A \ (A \ B) = A Ç B;
ж) A Ç (B \ C) = (A Ç B) \ (A Ç C);
з) (A È B) Ç (B È C) Ç (A È C) = (A Ç B) È (B Ç C) È (A Ç C);
и) А \ (В È С) = (А \ В) Ç (А \ С);
к) А \ (В Ç С) = (А \ В) È (А \ С);
л) A \ (B \ C) = (A \ B) È (AÇBÇC);
м) A Ç (B \ C) = (A Ç B) \ (A Ç C);
н) A È (B \ C) = (A È B) \ (A È C).
8. Для произвольных А, В, С Î Â(E) доказать или опровергнуть следующие тождества методом от противного.
а) (A \ (A \ B)) \ (A Ç B) = Æ;
б) А Ç (В \ А) = Æ;
в) (A Ç C) \ (С \ (С \ A) = Æ;
г) (A \ С) \ (A Ç 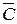 ) = Æ;
) = Æ;
д) 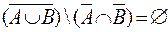 ;
;
е) 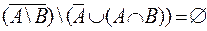 ;
;
ж) ((А Ç В) È (А Ç 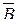 )) \ А = Æ.
)) \ А = Æ.
9. Докажите, что B È C = Æ, еслиB = Æ и C = Æ.
10. Покажите на примере, что выражение A È B Ç C требует использования круглых скобок.
11. Докажите что если B Í A & C Í A, то B È C Í A;и еслиAÍ B & A Í C, тоA Í B Ç C.
12. Докажите, что если C Í A, тоB Ç C Í A и C Í A È B.
13. Докажите, Â(A) Ç Â(B) = Â(A Ç B).
14. Справедливо ли тождество Â(A) È Â(B) = Â(A È B).Если нет приведите пример.
15. Справедливо ли тождество: { x | x Î Z & x = 2 m } Ç { x | x Î Z & x = 3 m } = { x | x Î Z & x = 6 m }, где m Î N.
16. Опровергните следующее утверждение: если А Ç В = А Ç С, то В = С.
17. Пусть
I - множество целых чисел, I = {...-1, 0, 1,...};
N - множество положительных целых чисел N = {0, 1, 2,...};
Np - множество отрицательных целых чисел Np = {..., -2, -1, 0};
E - множество четных чисел;
P - множество простых чисел.
Найдите: N Ç Np, I \ N, I \ Np, N È Np, I \ E, E Ç P.
18. Доказать, что А = В, следуя каждому из следующих условий:
а) A \ B = B \ A;
б) A È B = B Ç A;
в) A È C = B È C & A Ç C = B Ç C.
19. Доказать, что 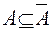 , если только A = Æи
, если только A = Æи 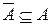 .
.
20. Используя диаграммы Венна, рассмотрите совместимость следующих утверждений.
а) (A Ç B) È C = A \ B и C Ç A = B Ç A;
б) (A \ (B \ C)) Í C È B и A Ç B Ç C = Æ и C \ B Í A;
с) (B \ A) Ç C ¹ Æ и C \ A Í C \ B.
21. Докажите следующие тождества:
а) (A È B) Ç (C È D) = (A Ç C) È (A Ç D) È (B Ç C) È (B Ç D);
б) А \ В = 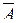 È (А Ç В);
È (А Ç В);
в) А \ (А \ (А \ В)) = А \ В;
г) А \ (А \ (А \ (А \ В))) = А Ç В;
д) A1 È A2 È... È An = (A1 \ A2) È (A2 \ A3) È... È (An-1 \ An) È (An \ A1) È (A1 Ç A2 Ç... Ç An) = A1 È (A2 \ A1) È (A3 \ (A1 È A2)) È (A4 \ (A1 È A2 È A3)) È... È (An \ (A1 È A2 È... È An-1)).
е) A1 Ç A2 Ç... Ç An = A1 \ [(A1 \ A2) È (A1 \ A3) È... È (A1 \ An)]
22. Упростите следующие выражения:
а) 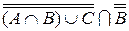 ;
;
б) 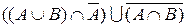 .
.
 2020-04-07
2020-04-07 250
250








