Доказательство тождеств с множествами позволяет получать записи минимальной длины для построения эффективных логических схем

 

Условность нужно соблюдать в частном, а порядок в общем.

Ж. Бернарден

Глава 3. Упорядоченные множества

Упорядоченное множество (кортеж), равенство кортежей, декартово произведение множеств, степень множества, операции над упорядоченными множествами, график, диагональ, инвертирование, проектирование и композиция упорядоченных множеств и графиков, функциональные и инъективные графики.

ЦЕЛИ

Освоив эту главу, студенты должны:

· знать определение упорядоченного множества (кортежа);

· уметь выполнять операции над кортежами;

· знать правила выполнения совместных операций над кортежами и множествами;

· уметь выполнять операции инверсии и композиции;

· уметь доказывать тождества с кортежами;

· иметь понятие о графиках и их проекциях на заданные оси;

· знать основные свойства графиков.

3.1. Кортеж (Упорядоченное множество)

Кортеж, как и множество, является исходным неопределенным понятием. Синонимами термину кортеж являются вектор и набор. Кортеж обозначается строчными греческими буквами. Компоненты кортежа — строчными латинскими буквами.

a = < 2, 2, 3, 4, 4 > — пример кортежа.

В этом примере кортеж a состоит из пяти компонент: “2”, расположенная на первом месте; “2”, расположенная на втором месте; “3”; расположенная на третьем месте; “4”, расположенная на четвертом месте; “4”, расположенная на пятом месте. Т.е. в отличие от множества, кортеж может иметь повторяющиеся элементы, но все эти элементы различны. Число компонент кортежа называется его длиной. Длиной кортежа может быть любое целое неотрицательное число. Компонента кортежа эквивалентна элементу множества. Кортеж a длины S записывается a = < a ₁, a ₂, a ₃,..., a _S >, то есть |a| = S.

Компоненты кортежа могут обозначать любые понятия, объекты, в том числе элементы множества или кортежа. Например, a = < 3, Æ, 2 x - 1, {2, 1}, <3, 7> > — кортеж длины 5. Первая компонента число - 3, вторая — пустое множество, третья — многочлен, четвертая — множество и пятая компонента — кортеж длины 2.

В отличие от элементов множества, компоненты кортежа могут частично или полностью совпадать. Например, b = < 4, 4, 4, 4, 4 > — кортеж длины 5. Кортеж длины 2 называется двойка или пара, длины 3 — тройка и так далее. Наряду с кортежами длины 2, 3, 4,... существуют кортежи длины 1. Например, g = < 6 >.

Кортеж, который не содержит компонентов в своем составе, называется пустым кортежем и обозначается a = < >. Длина этого кортежа равна нулю.

Говорят, что два кортежа равны (a = b), если a и b имеют одинаковую длину и каждая компонента кортежа a совпадает с каждой компонентой кортежа b.

Кортежи a и b неравны (a ¹ b), когда они имеют разную длину или отдельные компоненты кортежа a не совпадают с соответствующими компонентами кортежа b.

Для любых кортежей a, b, g справедливы утверждения:

· если a = b, то b = a,

· если a = b и b = g, то a = g.

Например, два кортежа a = < 3, 5 > и b = < 5, 3 > не равны между собой, а кортежи a = < 9, 10 > и b = < 9, 10 > — равны.

В отличие от множеств, порядок следования компонент кортежа существенен. Отметим, что иногда кортеж называют упорядоченным множеством. Теоретико-множественная запись равенства кортежей имеет следующий вид:

для кортежей длины два: a = < a, b >, b = < c, d >, a = b ® a = c & b = d;

для кортежей длины три: a = <a₁, a₂, a₃>, b = <b₁, b₂, b₃>, a = b ® a₁ = b₁ & a₂ = b₂ & a₃ = b₃.

Кортеж a называют кортежем над множеством М, если каждая компонента кортежа a принадлежит М. Согласно определению пустого кортежа, данный кортеж является кортежем над любым множеством, в том числе и над пустым множеством.

3.2. Декартово произведение

Декартовым произведением множеств А и В называется множество, состоящее из всех тех и только тех пар, т.е. кортежей длины 2, первая компонента которых принадлежит множеству А, а вторая — множеству В.

А × В — декартово произведение множеств А и В.

Из определения этого произведения следует, что для произвольного кортежа длины 2:например,< х ₁, х ₂>, принадлежащего декартову произведению множеств, истинно высказывание:

< х ₁, х ₂>ÎA × B ® х ₁ÎA & х ₂ÎB.

В том случае, если кортеж < y ₁, y ₂> не принадлежит декартову произведению, истинно высказывание:

< y ₁, y ₂>ÏA × B ® y ₁ÏA Ú y ₂ÏB.

Например, заданы множества А = { a, b }, B = { c, d, e }. Тогда декартово произведение этих множеств равно A × B = {<a, c>, <a, d>, <a, e>, <b, c>, <b, d>, <b, e>}.

Кортеж длины 2 <a, b> можно изобразить на координатной плоскости точкой, абсциссой которой является 1-й элемент кортежа, а ординатой — 2-й элемент кортежа.

Например, заданы множества A = {2, 3}, B = {1, 4}. Тогда A × B = {<2, 1>, <2, 4>, <3, 1>, <3, 4> }, B × A = {<1, 2>, <1, 3>, <4, 2>, <4, 3>} (рис. 3.1).

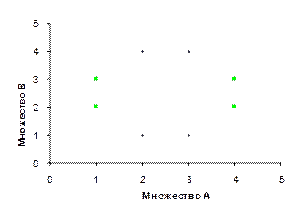
Рис. 3.1. Пример декартова произведения двух множеств (B ´ A – точки ¨; A ´ B – точки ■)

Аналогичным образом определяется декартово произведение трех, четырех и более множеств.

Декартовым произведением трех множеств А, В, С называется множество, состоящее из всех тех кортежей длины 3, 1-й элемент которых принадлежит множеству А, 2-й — множеству В, 3-й — множеству С. Например, если, A = {2, 3}, B = {a, b}, С = { x, y }. Тогда A × B × C = {<2, a, x >, <2, a, y >, <2, b, x >, <2, b, y >, <3, a, x >, <3, a, y >, <3, b, x >, <3, b, y >}.

Из определения декартова произведения следует, что А × В равно Æ, если А = Æ или В = Æ:

А × В = Æ ® А = Æ Ú В = Æ.

По аналогии можно утверждать, что произведение нескольких множеств равно пустому множеству тогда и только тогда, когда хотя бы одно из этих множеств пусто:

А₁ × А₂ × А₃ ×... × А_n = Æ ® А₁ = Æ Ú А₂ = Æ Ú А₃ = Æ Ú … Ú А_n = Æ.

Исходя из свойств кортежа, справедливо следующее: А × В ¹ В × А.

Операцию декартова произведения используют для определения степеней множества.

Пусть М — произвольное множество. Назовем S-той степенью множества М и обозначим М^S прямое декартово произведение S - одинаковых множеств, равных М. Для S = 2, 3, 4...

M^S = M × M × M ×... × M

     S – раз

По определению считают, что M¹ = M, M⁰ = < >. При S ³ 2 множество М^S является множеством всех кортежей длины S над множеством М.

Если М содержит n элементов и S ³ 2, то число элементов множества М^S равно n ^S, где n – число элементов множества М. Например, М = {a, b}, M⁰ = < >, M¹ = M, М² = {<a, a>, <a, a>, <b, a>, <b, b>}, M³ = {<a, a, a>, <a, a, b>, <a, b, a>, <a, b, b>, <b, a, a>, <b, a, b>, <b, b, a>, <b, b, b>}.

Декартово произведение двух множеств обладает следующими свойствами:

· X × Y ¹ Y × X                                           - некоммутативность;

· X × (Y × Z) = (X × Y) × Z = X × Y × Z   - ассоциативность;

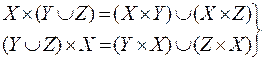· - дистрибутивность по объединению;

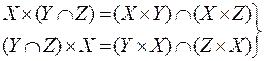· - дистрибутивность по пересечению;

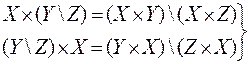·     - дистрибутивность по разности;

· (X × Y) Ç (W × Z) = (X Ç W) × (Y Ç Z).

Некоторые из перечисленных свойств следуют из определения декартова произведения. Для доказательства других свойств необходимо использовать методы доказательств тождеств с множествами.

3.3. Операция проектирования множеств

Введем еще одну операцию — операцию проектирования.

Операция проектирования унарна. Она применима не к двум множествам, а к одному множеству. Кроме этого, операция проектирования применима только к множеству кортежей одинаковой длины. Проекция множеств определяется через проекцию кортежей.

Определим понятие проекции кортежей.

Пусть задан кортеж a = < a ₁, a ₂,..., a _s > длины s, s > 0.

1) Пусть 1 £ i £ s. Тогда проекцией кортежа a на i -тую ось называется i -тая компонента кортежа a.

2) Пусть задано произвольное число q, такое, что 2 £ q £ s. И пусть задано число осей 1 £ i ₁ £ i ₂ £... £ i _q £ s. Тогда проекцией кортежа a на оси с номерами i ₁, i ₂,..., i _q называется кортеж < a _{i 1}, a _{i 2},..., a _{i q} >, который обозначается следующим образом: пр _{i 1, i 2,..., i q} a = < a _{i 1}, a _{i 2},..., a _{i q} >.

3) Проекцией кортежа a на пустое множество осей называется пустой кортеж. Аналогично проекцией пустого кортежа на пустое множество осей называется пустой кортеж.

Например, задан кортеж a = < 12, 15, 6, 7, 8 >, пр _{i 1} a = < 12 >, пр _{i 2} a = < 15 >, пр _{i 3} a = < 6 >, пр _{i 4} a = < 7 >, пр _{i 5} a = < 8 >, пр _{i 1, i 2} a = < 12, 15 >, пр _{i 1, i 5} a = < 12, 8 >, пр _{i 6, i 8} a = < >.

Определим понятие проекции множества. Как отмечено это понятие будет определено только для случая, когда проектируемое множество состоит из кортежей, причем все кортежи имеют одинаковую длину.

Проекция множества М — это множество проекций кортежей из М.

Пусть задано множество кортежей М длины s, s > 0.

1) Пусть 1 £ i £ s, тогда проекцией множества М на i -тую ось называется множество проекций кортежей из М на i -тую ось и обозначается: пр _i М.

2) Пусть задано произвольное число q, такое, что 2 £ q £ s, и задано число осей 1 £ i ₁ £ i ₂ £... £ i _q £ s. Тогда проекцией множества М на оси с номерами i ₁, i ₂,..., i _q называется множество проекций кортежей из М на оси с номерами i ₁, i ₂,..., i _q.

3) Проекцией множества М на пустое множество осей называется множество проекций кортежей из М на пустое множество: пр_ÆМ.

Рассмотрим пример. Пусть М = { < 1, 2, 3, 4, 5 >, < 2, 1, 3, 5, 5 >, < 3, 3, 3, 3, 3 >, < 3, 2, 3, 4, 3 >, < a, b, a, 1, a > }. Тогда пр₂М = { 2, 1, 3, 2, b }, пр_2,4М =    { < 2, 4>, < 1, 5>, < 3, 3>, < 2, 4>, < b, a> }, пр_6,7М = Æ.

Пусть М — произвольное множество, длина которого s, s ³ 2. Тогда множество М^s состоит из кортежей длины s и значит, его можно проектировать. Операция проектирования множества основана на описанных правилах построения проекций кортежей и множеств. Для любого натурального числа i, 1 £ i £ s проекция пр _i M^s = M

Согласно определению операции проектирования, можно сказать, что для произвольного кортежа <x, y>истинны следующие высказывания:

< x, y > Î A ® x Î пр₁A & y Î пр₂А,

x Ï пр₁A Ú y Ï пр₂А ® < x, y > Ï A.

Приведем основные свойства операции проектирования:

Пусть A Í X × Y, B Í X × Y, тогда для любых x Î X и y ÎY(" x Î X & y Î Y) истинно:

· ,

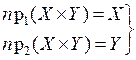· пр₁X² = пр₂X² = X,

· ,

· ,

· ,

· ,

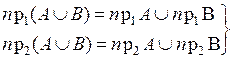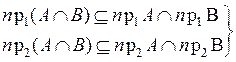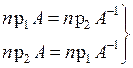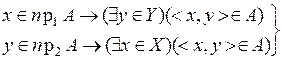· x Î пр₁A & y Î пр₂A ® ($ w Î Y)($ z Î X)(< x, w > Î A & < z, y > Î A).

В то же время в общем случае ложными являются следующие высказывания:

· ,

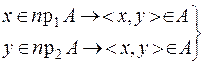· x Î пр₁A & y Î пр₂A ® < x, y > Î A,

· ,

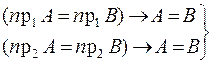· (пр₁A = пр₁B) & (пр₂A = пр₂B) ® A = B.

Некоторые из перечисленных высказываний следуют из определения прямого произведения. Для доказательства других свойств необходимо использовать методы доказательств тождеств с множествами.

Рассмотрим операции над кортежами. Известны две основные операции: инверсия кортежа и композиция кортежа.

1) Инверсия.

Инверсия кортежа определяется следующим образом. Пара < c, d > называется инверсией пары < a, b >, если c = b & d = a. Инверсия пары a обозначается a ^-1.

Например, a = < a, b >, тогда a ^-1 = < b, a >. (a ^-1)^-1 = a, ((a ^-1)^-1)^-1 = a ^-1. Тогда a ^{- n} = a и a ^{- ( n - 1)} = a ^-1, при n – четном.

2) Композиция.

Кортеж a = < x, y > называется композицией двух кортежей b = < x, z > и g = < z, y > и записывается a = b • g. Операция композиции справедлива, когда вторая компонента кортежа b совпадает с первой компонентой кортежа g. Здесь как бы происходит “склеивание” двух кортежей по компоненте z.

3.4. График

График — это множество каждый элемент которого является парой или кортежем длины 2. Множество Р называется графиком, если каждый элемент его пара.

Например, множество Р = {< a, b >, < a, 1>, < c, d >} является графиком.

Если М — произвольное множество, то М², а также любое множество С Í М² является графиком. В частности графиком является множество D² действительных чисел. Пусть заданы множества A и B, тогда А × В, С ÍА × В являются графиками.

Понятие графика является обобщенным. В принципе оно происходит от понятия графика функции.

Областью определения графика Р называется множество пр₁Р (проекция на первую ось (ось абсцисс) данного графика).

Областью значения графика называется множество проекций на вторую ось (ось ординат) (пр₂Р).

Легко видеть, что если Р — график, тогда если Р = Æ, то пр₁Р = Æ Ù пр₂Р = Æ.

Рассмотрим операции над графиками. Известны две основные операции: инверсия графика и композиция графика.

1) Инверсия.

Инверсия графика определяется через инверсию кортежа.

Инверсией графика Р называют множество инверсий пар из Р.

Например, Р = {< c, d >, < a, b >}, Р^-1 = {< d, c >, < b, a >}.

График Q называется инверсией графика Р, если $ a Î Q тогда и только тогда, когда a ^-1 Î Р, где a - произвольный кортеж.

В теоретико-множественном виде запишем:

a ^-1 Î Р ® a Î Р^-1,

a Î Р ® a ^-1 Î Р^-1

График Р называется симметричным, если он наряду с любой своей парой содержит ее инверсию.

Например, графикP = {< a, b >, < b, a >} является симметричным.

Пусть М — произвольное множество. Тогда считают DМ — множество всех пар вида < x, x >, где x присутствует во всем множестве М.

Таким образом, если М = { a, b }, то DМ = {< a, a >, < b, b >} — является симметричным графиком и называется диагональю.

2) Композиция.

График R является композицией двух графиков P и Q, а также < x, y > Î R, тогда и только тогда, когда $ z такое, что < x, z > Î P & < z, y > Î Q.

Переход от графиков P и Q к их композиции (P • Q) называется операцией композиции (или просто композицией) графиков P и Q.

Например, пусть Р = {< a, a >, < a, c >}, а Q = {< a, b >, < b, c > }, тогда P • Q = {< a, b >}.

Композиция графика Р и Æ равна Æ, то есть Р • Æ = Æ • Р = Æ.

Если М — произвольное множество и Р Í М², тогда

Р • DМ = DМ • Р = Р.

Если операцию композиции графиков сопоставить с умножением чисел, то роль нуля будет играть пустое множество, а роль единицы — диагональ (D).

Пусть <x, z> — произвольная пара из A • B. Тогда для нее справедливо высказывание:

< x, z > Î A • B ® ($ y Î (Y Ç W))(< x, y > Î A & < y, z > Î B).

Если некоторая пара < x, z > не принадлежит A • B, то истинно высказывание:

< x, z > Ï A • B ® (" y Î (Y Ç W))(< x, y > Ï A Ú < y, z > Ï B).

В операции композиции элемент y называется компонирующим элементом для пар < x, y > Î Aи< y, z > Î B. Если множество компонирующих элементов пусто, то и результат композиции является пустым множеством:

A • B = Æ ® пр₂A Ç пр₁B = Æ ® A • Æ = Æ • A = Æ.

Приведем свойства операции композиции:

* A • B ¹ B • A - некоммутативность;

*  A • (B • С) = (A • B) • С - ассоциативность;

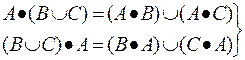* - дистрибутивность по объединению;

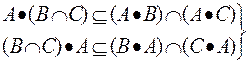* - дистрибутивность по пересечению;

*  (A • B)^-1 = B^-1 • A^-1

Некоторые тождества следуют из определения операции композиции, остальные тождества доказываются уже известными методами.

Используя методы доказательства тождеств с множествами, можно доказать, что для любых трех графиков P, Q, R справедливо

(P • Q) • R = P • (Q • R).

Докажем это тождество:

I. Необходимость. Предположим, что существует произвольный кортеж < a, b >, принадлежащий левой части тождества. Попытаемся доказать, что он принадлежит правой части тождества.

< a, b > Î (P • Q) • R ® < a, z > Î (P • Q) & < z, b > Î R ® < a, x > Î P & < x, z > Î Q & < z, b > Î R ® < a, x > Î P & < x, b > Î (Q • R) ® < a, b > Î (P • (Q • R)).

Следовательно, первая часть доказана.

II. Достаточность. Предположим, что существует произвольный кортеж < a, b >, принадлежащий правой части тождества. Попытаемся доказать, что он принадлежит левой части тождества.

< a, b > Î (P • (Q • R)) ® < a, x > Î P & < x, b > Î (Q • R) ® < a, x > Î P & (< x, d > Î Q & < d, b > Î R) ® < a, x > Î P & < x, d > Î Q & < d, b > Î R ® < a, d > Î (R • Q) & < d, b > Î R ® < a, b > Î ((P • Q) • R).

Следовательно, вторая часть доказана. Тогда делаем вывод, что исходное тождество справедливо.

Доказанное тождество позволяет определить композицию трех графиков P, Q, R, понимая под этим результат любой перестановки скобок, приводящей к последовательному попарному компонированию графиков. При компонировании трех графиков возможно только два способа расстановки скобок. Это позволяет определить композицию произвольного попарного компонирования графиков.

Операции композиции и инверсии связаны следующим равенством:

(P • Q)^-1 = Q^-1 • P^-1.

Докажем справедливость тождества (P • Q)^-1 º P^-1 • Q^-1:

1. Необходимость. Пусть < a, b > Î (P • Q)^-1 ® < b, a > Î (P • Q) ® < b, x > Î P & < x, a > Î Q ® < x, b > Î P^-1 & < a, x > Î Q. Получить теперь P^-1 • Q^-1 в общем виде невозможно, следовательно, исходное тождество неверно.

Докажем теперь справедливость другого тождества (P • Q)^-1 º Q^-1 • P^-1:

1. Необходимость. Пусть < a, b > Î (P • Q)^-1 ® < b, a > Î (P • Q) ® < b, x > Î P & < x, a > Î Q ® < x, b > Î P^-1 & < a, x > Î Q ® < a, x > Î Q^-1 & < x, b > Î P^-1 ® < a, b > Î (Q^-1 • P^-1).

1. Достаточность. Пусть < a, b > Î (Q^-1 • P^-1) ® < a, x > Î Q^-1 Ù < x, b > Î P^-1 ® < x, a > Î Q Ù < b, x > Î P ® < b, x > Î P Ù < x, a > Î Q ® < b, a > Î (P • Q) ® < a, b > Î (P • Q)^-1.

Следовательно, это тождество справедливо.

Рассмотрим два основных свойства графиков.

График Р называется функциональным, если в нем нет пар с одинаковыми первыми и разными вторыми компонентами.

Например, график Р = {< b, a >, < c, a >, < d, а >} является функциональным графиком.

На рис. 3.2 (а, б) приведены примеры функциональных графиков.

P₁ = {< a, 4>}, P₂ = {< a, 2>, < b, 3>, < c, 3>, < d, 4>}.

              

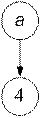
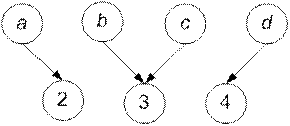
                        а                                  б

Рис.3.2. Примеры функциональных графиков

График Р называется инъективным, если в нем нет пар с различными первыми и одинаковыми вторыми компонентами.

Например, Р = {< a, b >, < a, c >, < a, d >} является инъективным графиком.

На рис. 3.3 (а, б) приведены примеры инъективных графиков.

P₃ = {< a, 1>}, P₄ = {< b, 2>, < c, 3>, < c, 4>}.

     

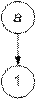
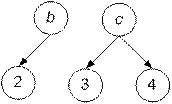
а                               б

Рис. 3.3. Примеры инъективных графиков

Композиция функциональных графиков есть функциональный график, т.е. композиция сохраняет функциональность.

Композиция инъективных графиков инъективна. Доказательство данного утвержденияможно найти в литературе, приведенной в конце раздела.

Итак, говорят, что график P функционален тогда и только тогда, когда Р^-1 инъективен. График Р инъективен тогда и только тогда, когда Р^-1 функционален.

Примеры РЕШЕНИЯ ЗАДАЧ

Пример 3.1. Пусть заданы множества А = { a, b }; B = {3, 1, 2}; C = { a, b }.

Ответ: A × B × C = {< a,1, a >, < a, 1, b >, < a, 2, a >, < a, 2, b >, < a, 3, a >, < a, 3, b >, < b, 1, a >, < b, 1, b >, < b, 2, a >, < b, 2, b >, < b, 3, a >, < b, 3, b >}.

Пример 3.2. Пусть задано произвольное множество A = { a, b }.Найти третью степень заданного множества.

Ответ: A³ = A × A × A = { a, b } × { a, b } × { a, b } = {< a, a, a >; < a, a, b >; < a, b, a >; < a, b, b >; < b, a, a >; < b, a, b >; < b, b, a >; < b, b, b >}.

Пример 3.3. Доказать истинность тождества методом взаимного включения:

C × (Y È Z) = (X × Y) È (X × Z).

Доказательство:

1.Необходимость.Пусть для произвольного кортежа < x, y > истинно высказывание:

< x, y > Î X × (Y È Z) ® x Î X & y Î (Y È Z) ®

(согласно свойству дистрибутивности)

x Î X & (y Î Y Ú y Î Z) ®

(по определению операции объединения множеств)

x Î X & y Î Y Ú x Î X & y Î Z ®

(согласно дистрибутивному закону)

< x, y > Î (X × Y) Ú < x, y > Î (X × Z) ® < x, y >Î((X × Y) È (X × Z)).

(исходя из свойства дистрибутивности)

Таким образом, прямое включение доказано.

2. Достаточность.

Аналогично доказывается обратное включение:

< x, y > Î ((X × Y) È (X × Z)) ® < x, y > Î (X × Y) Ú < x, y > Î (X × Z) ®

(x Î X & y Î Y) Ú (x Î X & y Î Z) ® x Î X & (y Î Y Ú y Î Z) ®

x Î X & y Î (Y È Z) ® < x, y > Î (C × (Y È Z)).

Обратное включение доказано. Таким образом, поскольку оба включения истинны, истинно и исходное тождество.

 

Пример 3.4. Доказать справедливость тождества методом от противного:

((X × Y) Ç (W × Z)) \ ((X Ç W) × (Y Ç Z)) = Æ.

Доказательство: Предположим, что данное выражение не верно и, следовательно, данное множество не равно пустому. Тогда должен существовать хотя бы один кортеж < x, y >, принадлежащий исходному множеству:

< x, y > Î [(X × Y) Ç (W × Z)] \ [(X Ç W) × (Y Ç Z)] ®

< x, y > Î ((X × Y) Ç (W × Z)) & < x, y > Ï ((X Ç W) × (Y Ç Z)) ®

(согласно определению операции разности множеств)

[< x, y > Î (X × Y) & < x, y > Î (W × Z)] & [ x Ï (X Ç W) Ú y Ï (Y Ç Z)] ®

(согласно определению операции пересечения множеств)

(x Î X & y Î Y & x Î W & y Î Z)&(x Ï X Ú x Ï W Ú y Ï Y Ú y Ï Z) ®

(согласно дистрибутивному закону алгебры логики)

(x Î X & y Î Y & x Î W & y Î Z & x Ï X) Ú (x Î X & y Î Y & x Î W & y Î Z & x Ï W) Ú (x Î X & y Î Y & x Î W & x Î Z & y Ï Y) Ú (x Î X & y Î Y & x Î W & y Î Z & y Ï Z).

В полученном выражении в каждой из составляющих его конъюнкций мы обнаружили противоречие. Например, x Î X & x Ï X. То есть очевидно, что наше предположение ложно, а значит исходное тождество истинно. Что и требовалось доказать.

 

Пример 3.5. Пусть задан график: А = {<1, 2>, <2, 3>, <2, 5>, <3, 4>, <3, 6>}. Найти его инверсию.

Ответ: А^-1 = {<2, 1>, <3, 2>, <5, 2>, <4, 3>, <6, 3>}.

Пример 3.6. Пусть задан график: А = {<1, 2>, <1, 3>, <2, 3>, <3, 3>, <3, 4>}. Найти первую и вторую проекции заданного графика.

Ответ: пр₁А = {1, 2, 3}, пр₂A = {2, 3, 4}.

Пример 3.7. Доказать справедливость тождества методом взаимного включения:

Ответ: пр₁(A Ç B) Í пр₁A Ç пр₁B

Доказательство:

1. Необходимость. Предположим, что исходное высказывание справедливо, тогда для любого элемента x, принадлежащего данной проекции, справедливо следующее высказывание:

x Î пр₁(A Ç B) ® ($ y Î Y)(< x, y > Î (A Ç B)) ®

< x, y > Î A & < x, y > Î B ® x Î пр₁A & x Î пр₁B ® x Î (пр₁A Ç пр₁B)

(согласно определению операции проектирования)

Таким образом, прямое включение доказано.

2. Достаточность. Теперь докажем, что в общем случае обратное включение невозможно. Пусть для любого x истинно:

x Î (пр₁A Ç пр₁B) ® x Î пр₁А & x Î пр₁В ®

($ y Î Y)(< x, y > Î A) & ($ z Î Y)(< x, z > Î B).

Поскольку в общем случае неизвестно, совпадают ли y и z, обратное включение, в общем случае, доказать невозможно.

 

Пример 3.8. Привести пример, демонстрирующий справедливость включения пр₁(A Ç B) Í пр₁A Ç пр₁B.

Решение: Пусть заданы множества А = {<1, 2>}; B = {<1, 3>}. Очевидно, что пр₁(A Ç B) = прÆ = Æ, в то время как пр₁A Ç пр₁B = {1} Ç {1} = {1}. Æ Í {1}. Таким образом, пр₁(A Ç B) ¹ пр₁A Ç пр₁B. В случае, если A Ç B ¹ Æ, исходное высказывание преобразуется в равенство.

 

Пример 3.9. Привести пример того, что высказываниеПр₁А = Пр₁В ® A = B - ложно.

Решение: Пусть заданы множества: А = {<1, 2>, <1, 3>, <1, 4>, <5, 6>, <5, 7>}; B = {<1, 6>, <1, 7>, <5, 2>, <5, 3>, <5, 4>}.

Для доказательства построим проекции заданных множеств. Очевидно, что проекции множеств равны между собой: пр₁А = пр₁В = {1, 5}; пр₂А = пр₂В = {2, 3, 4, 6, 7}, в то время как множества Aи Bне равны. Следовательно, задание выполнено.

 

Пример 3.10. Заданы произвольные графики:А = {< a, a >, < b, e >, < c, k >, < f, g >}; B = {< a, d >, < c, b >, < g, f >, < e, c >, < b, b >}. Найти композиции графиков A • B иB • A.

Решение: Для того, чтобы найти композицию графиков A и B, выбираем поочередно из кортежей множества вторые компоненты A, сравниваем со всеми первыми компонентами кортежей множества B. В тех случаях, когда обнаруживается совпадение, выполняем композицию соответствующих кортежей. Например, берем вторую компоненту первого кортежа из множества A. Это компонента a. Сравниваем ее поочередно со всеми первыми компоентами кортежей множества B. Находим совпадение с первой компонентой первого кортежа множества B. В результате получаем композицию этих двух кортежей:

< a, a > • < a, d > = < a, d >.

Затем выбираем вторую компоненту следующего кортежа множества A и сравниваем ее со всеми первыми компонентами кортежей множества B:

< b, e > • < e, c > = < b, c >.

Процесс продолжается аналогично до тех пор, пока не будут выявлены все совпадения и построены все композиции кортежей. В результате мы получим композицию множеств A и B. Для построения композиции множеств B и A необходимо аналогичным образом сравнить вторые компоненты кортежей множества B с первыми компонентами кортежей множества A.

Ответ: A • B = {< a, d >, < b, c >, < f, f >}, B • A = {< c, e >, < g, g >, < e, k >, < b, e >}.

Пример 3.11. Доказать справедливость высказывания методом взаимного включения:

A • (B È С) = (A • B) È (A • С).

Доказательство:

1. Необходимость. Предположим, что данное тождество справедливо. Тогда существует произвольная пара:

< x, z > Î (A • (B È С)) ® ($ y)(< x, y > Î A & < y, z > Î (B È С)) ®

(согласно определению операции композиции)

< x, y > Î A & (< y, z > Î B Ú < y, z > Î С) ®

(по определению операции объединения множеств)

(< x, y > Î A & < y, z > Î B) Ú (< x, y > Î A & < y, z > Î С) ®

(согласно дистрибутивному закону)

(< x, z > Î A • B) Ú (< x, z > Î A • С) ® < x, z > Î ((A • B) È (A • С)).

То есть прямое включение доказано.

2. Достаточность. Теперь докажем обратное включение. Предположим, что существует пара:

< x, z > Î ((A • B) Ú (A • С)) ® < x, z > Î (A • B) Ú < x, z > Î (A • С) ®

($ y)(< x, y > Î A & < y, z > Î B) Ú ($ w)(< x, w > Î A & < w, z > Î С) ®

(так как в общем случае, компонирующие элементы не обязательно совпадают)

(< x, y > Î A & < y, z > Î (B È С))Ú (< x, w > Î A & < w, z > Î (B È С)) ®

< x, z > Î (A • (B È С)) Ú < x, z >Î(A • (B È С)) ® < x, z >Î(A • (B È С)).

Обратное включение также доказано, следовательно, исходное тождество верно.

 

Пример 3.12. Доказать справедливость высказывания методом взаимного включения:

A • (B Ç С) Í (A • B) Ç (A • С).

Доказательство: Доказательство прямого включения проводится аналогично доказательству, рассмотренному выше, и интереса не представляет. Рассмотрим обратное включение и докажем, что оно в общем случае не имеет места.

2. Достаточность. Предположим, что справедливо тождество:

(A • B) Ç (A • С) Í A • (B Ç С).

Тогда существует произвольная пара:

< x, z > Î ((A • B) Ç (A • С)) ® < x, z > Î (A • B) & < x, z > Î (A • С) ®

($ y)(< x, y > Î A & < y, z > Î B) & ($ w)(< x, w > Î A & < w, z > Î С)

(в общем случае y ¹ w, значит продолжить цепочку преобразований, чтобы доказать обратное включение не возможно).

Таким образом, обратное включение в общем случае не доказывается.

Следовательно, высказывание A • (B Ç С) Í (A • B) Ç (A • С) - истинно.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Приведите примеры кортежей.

2. Как образуется прямое произведение множеств?

3. В каком случае число элементов прямого произведения множеств равняется нулю?

4. Что представляет собой прямое произведение двух множеств с точки зрения теории множеств?

5. Какими свойствами обладает декартово произведение множеств?

6. В чем заключается операция проектирования множеств?

7. В каком случае упорядоченная пара не принадлежит прямому произведению двух множеств?

8. Для каких множеств А и В справедливо: Х × Y = Y × Х?

9. Равны ли множества: пр₁А È пр₂А и А, если: А Í Х × Y?

10. Что такое инверсия упорядоченного множества А?

11. Для какого множества А Í Х × Y справедливо: А=А^-1?

12. В каком случае существует композиция двух произвольных упорядоченных множеств А и В?

13. В каком случае справедливо тождество: А • В = В • А?

14. В каких случаях справедливо тождество: А • А = А?

15. Что такое график?

16. Приведите основные операции над графиками.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1. Найти прямое произведение множеств Х иY, если:

а) Х = {{ a, b }, c, { d, e, f }}; Y = { g, h };

б) Х = { а, b, c }; Y = Æ;

в) Х = {2, 4, 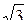}; Y = {{Æ}, a, b }.

2. Найти n -ю степень множества Х, если:

a) Х = { x }, n = 5;                             в) Х = {{Æ}, y }, n = 2;

б) Х = { a, b }, n = 3;                         г) Х = 0, n = 3.

3. Доказать, что для произвольных множеств Х, У, W, Z, справедливы следующие высказывания:

а) (Y È Z) × X = (Y × X) È (Z × X);

б) Х × (Y Ç Z) = (Х × Y) Ç (Х × Z);

в) Х × (Y \ Z) = (Х × Y) \ (Х × Z);

г) (Х × Y) È (W × Z) Í (X È W) × (Y È Z);

д) (Х È Y) × (W È Z) = (X × W) È (Y × W) È (X × Z) È (Y × Z).

4. Равны ли множества Пр₁A È Пр₂A = A, если A Í Х × Y?

5. Для каких множеств А и В, справедливо А × В = В × А?

6. Для какого множества справедливо: A = А^-1, если AÍ Х × Y?

7. Доказать или опровергнуть, что для множеств A и B, где A Í Х × Y, B Í Х × Y справедливы следующие высказывания:

а) Пр₁(A \ B) = Пр₁A\ Пр₁B;           д) Пр₁(A \ B) ^-1 = Пр₂A \ Пр₂B;

б) Пр₁(A È B) ^-1 = Пр₂A È Пр₂B;   е) (A È B) ^-1 = А^-1 È B^-1;

в) Пр₁(A È B) = Пр₂A^-1 È Пр₂B^-1; ж) (A Ç B) ^-1 = A^-1 Ç B^-1;

г) (A \ B) ^-1 = A^-1 \ B^-1.

8. Доказать или опровергнуть, что для множеств A, Bи С, где A Í Х × Y, B Í Х × Y, С Í Х × Y справедливы следующие тождества:

а) (B È C) • A = (B • A) È (C • A);

б) A • (B \ C) = (A • B) \ (A • C).