Проблема континуума: существует ли промежуточное множество, содержащее больше элементов, чем множество натуральных чисел, и меньшее, чем множество точек на прямой

Направляя свое внимание исключительно в одну точку, мы можем легко ограничить нашу способность схватывать вещи и никогда не достигнем той дальнозоркости, которую дает нам широкий, хотя, быть может, и менее точный взгляд.

Г. Бокль

Глава 7. Основные понятия теории мультимножеств

Понятие мультимножества, компоненты мультимножеств, определение и способы задания мультимножеств,основные характеристики мультимножеств, операции над мультимножествами

ЦЕЛИ

Освоив эту главу студенты должны:

· иметь понятия о мультимножествах;

· знать основные характеристики мультимножеств;

· знать способы задания мультимножеств;

· уметь выполнять операции над мультимножествами.

7.1. Понятие мультимножества

Мы рассмотрели конечные множества, в которых отсутствуют повторяющиеся элементы. В кортежах возможны повторяющиеся элементы, но при этом значение каждого элемента определяется его местоположением. В задачах искусственного интеллекта начинают использоваться объекты с повторяющимися элементами. Материалы данной главы основаны на монографии А.Б. Петровского, приведенной в списке литературы.

Мультимножество - это множество с повторяющимися элементами, где один и тот же элемент может присутствовать многократно. Особенностью мультимножества является понятие кратности вхождения элемента. Элементы мультимножеств будем обозначать строчными буквами с подстрочным индексом М: a_М, b_М,..., мультимножества - прописными буквами с подстрочным индексом М – А_М, В_М,...

Примером мультимножеств могут служить, например, следующие совокупности элементов а, b, с, d, e, f, g, h:

A_М = { a, b, a, d, e, c, a, b, h, h }, B _М = { d, d, e, b, b, d, e, e, h }, C_М = { a, a, d, a, c, a, a, e, c, c, g, g, g }.

Порядок следования элементов в мультимножестве считается несущественным. Тогда приведенные мультимножества А, В, С можно переписать следующим образом:

A_М = {3 a, 2 b, c, d, e, 2 h },

B_М = {2 b, 3 d, 3 e, h },

C_М = {5 a, 3 c, d, e, 3 g },

Отметим, что отсутствующие элементы не указываются в записи мультимножества.

Приведем формальное определение мультимножества, данное А.Б. Петровским. Мультимножеством А_М,определенном на множестве А = { x ₁, x ₂,...}, все элементы x_i которого различны, называется совокупность групп одинаковых элементов

A_М = { k ₁ x ₁, k ₂ x ₂,...}, x_i Î А.

Группу одинаковых элементов k_ix_i называют компонентой мультимножества, элементы x_i, входящие в компоненту k_ix_i, - экземплярами элементов мультимножества. Функция k_i, принимающая числовые значения, определяет число вхождений элемента x_i Î А в мультимножество А_М или «вес» элемента x_i в мультимножестве А_М. Ее также называют функцией кратности или функцией числа экземпляров мультимножества А_М. Другими словами, мультимножество - это множество, состоящее из различных групп одинаковых экземпляров элементов.

Говорят, что элемент х_i принадлежит мультимножеству А_М (обозначается х_i Î А_М) и в мультимножестве А_М имеется ровно k экземпляров элемента х_i тогда и только тогда, когда кратность элемента х_i равна k_ix_i > 0. Когда кратность элемента х_i равна нулю k_ix_i = 0, тогда говорят, что элемент х_i не содержится в мультимножестве А_М (обозначается х_i Ï А_М). Тем самым принадлежность элемента х_i мультимножеству А_М определяется значением функции кратности.

Если все мультимножества семейства Q(А_М) = { А 1 _М, А 2 _М,...} образуются из элементов одного и того же множества G = { x ₁, x ₂,...}, то множество G называется порождающим множеством или доменом для семейства Q(А_М).В качестве порождающего множества G может выступать любое непустое (конечное или бесконечное) множество.

Основными характеристиками мультимножества являются мощность и размерность. Мощностьмультимножества А_М определяется как общее число экземпляров всех его элементов

а размерность мультимножества А - как общее число различных элементов

Размерность мультимножества не превосходит его мощности и мощности домена / А_М / £ | А_М |, / А_М / £ | G |. Мощность мультимножества | А_М |в общем случае не связана с мощностью домена | G |. Конечные мультимножества, имеющие мощность т и состоящие из т элементов (считая повторения), называют т-кардинальными мультимножествами или т-мультимножествами, а имеющие размерность п и состоящие из п компонент - n-мерными мультимножествами.

Высотой или пиковым значениеммультимножества А_М называется максимальное значение его функции кратности k_i, а элемент , для которого функция кратности k_A максимальна, - пиком или пиковым элементом мультимножества А_М.

Мультимножество удобно изображать графически в виде ступенчатой гистограммы, по оси абсцисс которой расположены элементы основного множества A или домена G, а по оси ординат отложены значения k_i (x_i) функции кратности, показывающие количество экземпляров элемента х_i в мультимножестве А_М. Таким образом, каждый столбец гистограммы соответствует определенной компоненте мультимножества А_М. Ширина гистограммы равна размерности / А_М / мультимножества, а высота гистограммы есть высота мультимножества А_М. Мощность мультимножества | А_М | будет численно равна площади фигуры, ограниченной гистограммой.

Для мультимножеств справедливы теоретико-множественные понятия, введенные для множеств.

Рассмотрим возможные способы сопоставления мультимножеств, обусловленные особенностями их различных характеристик. Мультимножества А_М и В_М называются равными (А_М = В_М), если k_i (x_i) = k_j (x_j) для всех элементов x_i, x_j Î G, k_i (x_i) Î А_М, k_j (x_j) Î B_М. В противном случае эти мультимножества неравны. Для равных мультимножеств имеем | A | = | В |, / A / = / B /.

Мультимножества А и В называют равномощными, если | А | = | В |. Например, мультимножества A_М = {3 a, 2 b }, B_М = {2 a, 3 b } являются равномощными, так как мощность мультимножества A_М = 5 и мощность мультимножества B_М = 5, а мультимножества C_М = {3 d, e }, D_М = { e, 2 d } – неравными, т.к. 4 ¹ 3.

Мультимножества А и В называют равноразмерными, если / A / = / B /. Например, мультимножества A_М = {3 a, 2 b, c }, B_М = {2 a, 2 b, 2c } являются равноразмернымимощными, так как число различных экземпляров мультимножества / A_М / = / B_М / = 3, а мультимножества C_М = {3 d, e }, D_М = { e, 2 d } – неравными, т.к. 4 ¹ 3.

Мультимножества А_M и В_M называют равными, если они равномощны и равноразмерны.

Говорят, что мультимножество В_M содержится или включено в мультимножество А_M (В_M Í А_M), если k_jx_j £ k_ix_i, для каждого элемента x_i, x_j Î G, k_ix_i Î А_М, k_jx_j Î B_М. Мультимножество В_M называется тогда подмультимножеством мультимножества А_M, а мультимножество А_M - надмультимножеством мультимножества В_M. В этом случае | В | £ | A |, / B / £ / A /. Как и в случае обычных множеств, одновременное выполнение условий В_M Í А_M и А_M Í В_M влечет равенство мультимножеств А_M = В_M.

Замечание. Включение мультимножества обладает свойствами рефлексивности (А_M Í А_M) и транзитивности (А_M Í В_M, В_M Í С_M Þ A_M Í С_M), а значит, является отношением предпорядка.

7.2. Операции над мультимножествами

Над мультимножествами определены следующие основные операции: объединение, пересечение, арифметическое сложение, арифметическое вычитание, дополнение, симметрическая разность, умножение на число, арифметическое умножение и возведение в арифметическую степень, прямое произведение и возведение в прямую степень.

Объединениеммультимножеств А_М и В_М называется мультимножество, состоящее из всех элементов, которые присутствуют хотя бы в одном из мультимножеств, и кратность каждого элемента равна максимальной кратности соответствующих элементов в объединяемых мультимножествах:

C_M = A_M È B_M = { max (k_ix_i, k_jx_j)}, k_ix_i Î А_М, k_jx_j Î B_М.

Другими словами, производится попарное сравнивание каждого экземпляра мультимножеств и в каждой паре выбирается экземпляр наибольшим значением функции кратности.

Например, заданы мультимножества A_М = {3 a, 2 с, d }, B_М = {3 b, 2 d, 2e }. Тогда их объединение C_M = {3 a, 3 b, 2 с, 2 d, 2e }.

Отметим, что можно выполнять операцию объединения произвольного числа мультимножеств.

Объединением произвольного числа мультимножеств Ai_M, называется мультимножество

A 1 _M È A 2 _M È … È An_M = { max (k_ix_i, k_jx_j, …, k_nx_n)}, k_ix_i Î А1_М, k_jx_j Î А2_М, …, k_nx_n Î Аn_М

Например, заданы мультимножества A1_М = {2 a, 3 с, d }, A2 _М = {2 b, 2 d, e }, A3_М = { a, 3 b, 2 с, 3 d, 4f }. Тогда их объединение C_M = {2 a, 3 b, 3 с, 3 d, e, 4 f }.

Пересечениеммультимножеств А_М и В_М называется мультимножество, состоящее из всех элементов, которые одновременно присутствуют в каждом из мультимножеств, и кратность каждого элемента равна минимальной кратности соответствующих элементов в пересекаемых мультимножествах:

C_M = A_M Ç B_M = { min (k_ix_i, k_jx_j)}, k_ix_i Î А_М, k_jx_j Î B_М.

То есть производится попарное сравнивание каждого экземпляра мультимножеств и в каждой паре выбирается экземпляр с наименьшим значением функции кратности.

Например, заданы мультимножества A_М = {3 a, 2 b, 4 c }, B_М = {3 b, 2 c, 2d }. Тогда их пересечение C_M = {2 b, 2 с }.

Пересечением произвольного числа мультимножеств Ai_M, называется мультимножество

A 1 _M Ç A 2 _M Ç … Ç An_M = { min (k_ix_i, k_jx_j, …, k_nx_n)}, k_ix_i Î А1_М, k_jx_j Î А2_М, …, k_nx_n Î Аn_М.

Например, заданы мультимножества A1_М = {2 a, 3 с, d }, A2 _М = {2 b, 2 d, e }, A3_М = {4 a, 3 b, 2 с, 3 d, f }. Тогда их пересечение C_M = {2 a, d }.

Арифметической суммоймультимножеств А_М и В_М называется мультимножество, состоящее из всех элементов, которые присутствуют хотя бы в одном из мультимножеств, и кратность каждого элемента равна сумме кратностей соответствующих элементов в складываемых мультимножествах:

C_M = A_M + B_M = { kx | kx = k_ix_i + k_jx_j }, k_ix_i Î А_М, k_jx_j Î B_М.

Например, заданы мультимножества A_М = {3 a, 2 b, 4 c }, B_М = {3 b, 2 c, 2d }. Тогда их арифметическая сумма C_M = {3 a, 5 b, 6 с, 2 d }.

Суммой произвольного числа мультимножеств Ai_M, называется мультимножество

A 1 _M + A 2 _M + … + An_M = { kx | kx = k_ix_i + k_jx_j + … + k_nx_n }, k_ix_i Î А1_М, k_jx_j Î А2_М, …, k_nx_n Î Аn_М.

Например, заданы мультимножества A1_М = {2 a, с, d }, A2 _М = {2 b, 2 d, e }, A3_М = {2 a, 3 b, 2 с, 3 d, 2 f }. Тогда их сумма C_M = {4 a, 5 b, 3 с, 6 d, e, 2 f }.

Арифметической разностьюмультимножеств А_М и В_М называется мультимножество, состоящее из тех элементов мультимножества А_М, кратность которых превышает кратность соответствующих элементов в мультимножестве В_М. Кратность каждого элемента результирующего множества равна разности кратностей соответствующих элементов в вычитаемых мультимножествах:

C_M = A_M - B_M = , k_ix_i Î А_М, k_jx_j Î B_М.

Например, заданы мультимножества A_М = {3 a, 2 b, c, 4 d }, B_М = {2 a, 3 b, 2 c, 2 d }. Тогда их арифметическая разность C_M = { a, 2 d }.

Операция разности мультимножеств определена только для двух мультимножеств. При этом если A_М Í B_М, то A_М - B_М = Æ. Справедливо и обратное утверждение: если A_М - B_М = Æ, то A_М Í B_М.

Симметрической разностьюмультимножеств А_М и В_М называется мультимножество, состоящее из тех элементов мультимножеств А_М и В_М, кратности которых различны. Кратность каждого элемента результирующего мультимножества равна модулю разности кратностей соответствующих элементов в вычитаемых мультимножествах:

C_M = A_M D B_M = { kx | kx = | k_ix_i - k_jx_j |}, k_ix_i Î А_М, k_jx_j Î B_М.

Например, заданы мультимножества A_М = { a, 2 b, 3 c, 4 d }, B_М = {3 a, 2 b, 3 c, 2 d }. Тогда их симметрическая разность C_M = {2 a, 2 d }.

Cимметрическая разность мультимножеств применима только к двум мультимножествам.

Дополнениеммультимножества A_М до универсума Z называется мультимножество, состоящее из элементов, кратность которых равна разности кратностей соответствующих элементов в универсуме Z и дополняемом мультимножестве А_М. Под универсумом в данном случае понимается некоторое мультимножество Z, такое, что все остальные мультимножества являются подмультимножествами данного множества Z.

Из определений пустого мультимножества и дополнения мультимножества следует, что пустое мультимножество Æ и универсум Z взаимно дополняют друг друга: , .

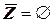Арифметическим произведением мультимножеств А_М и В_М называется мультимножество, состоящее из элементов, которые одновременно присутствуют в каждом из мультимножеств, и их кратность равна произведению кратностей соответствующих элементов в перемножаемых мультимножествах:

C_M = A_M • B_M = { kx | kx = k_ix_i • k_jx_j }, k_ix_i Î А_М, k_jx_j Î B_М.

Например, заданы мультимножества A_М = { a, 2 b, 3 d, 4 f }, B_М = {2 b, 3 c, d, 4 e, 3 f }. Тогда их арифметическое произведение C_M = {4 b, 3 d, 12 f }.

Арифметическим произведением произвольного числа мультимножеств Ai_M называется мультимножество

A 1 _M • A 2 _M • … • An_M = { kx | kx = k_ix_i • k_jx_j • … • k_nx_n }, k_ix_i Î А1_М, k_jx_j Î А2_М, …, k_nx_n Î Аn_М.

Например, заданы мультимножества A1_М = {3 a, с, 4 d }, A2 _М = {2 b, d, e }, A3_М = {2 a, 3 b, 2 с, 3 d, 2 f }. Тогда их арифметическое произведение C_M = {6 a, 12 d }.

Арифметической п-ой степенью мультимножества А_М называется арифметическое произведение п одинаковых мультимножеств А_М:

.

Произведением мультимножества А_М на целое число h или репродукцией мультимножества А_М называется мультимножество, состоящее из элементов мультимножества А_М, причем кратность каждого элемента увеличена в h раз:

h • А_М = { h • kx }.

Репродукцию мультимножества можно также представить как сумму h одинаковых мультимножеств А_М: h • А_М = А_М +... + А_М (h раз).

Прямым произведением мультимножеств А_М и В_М называется мультимножество, состоящее из всех упорядоченных пар элементов < x_i, х_j > таких, что первый элемент каждой пары является элементом первого сомножителя x_i Î А_М, второй элемент пары - элементом второго сомножителя х_j Î В_М и кратность каждой пары < x_i, х_j > равна произведению кратностей элементов x_i и х_j в перемножаемых мультимножествах:

C_M = A_M ´ B_M = { k_{A ´ B} < x_i, х_j > | k_{A ´ B} = k_ix_i • k_jx_j, x_i Î А_М, х_j Î В_М }.

Например, заданы мультимножества A_М = { a, 2 b, 3 с }, B_М = { d, 4 e }. Тогда их прямое произведение C_M = {< a, d >; 4< a, e >; 2< b, d >, 8< b, d >, 3< c, d >, 12< c, e >}.

Прямым произведением конечного числа мультимножеств Ai_M, называется мультимножество, состоящее из всех n -элементных кортежей < x ₁, …, х_n > таких, что i -ый элемент кортежа является элементом i -го сомножителя x_i Î A _i, и кратность каждого кортежа равна произведению кратностей элементов в перемножаемых мультимножествах:

A 1 _M ´ A 2 _M ´ … ´ An_M = { k < x ₁, …, х_n > | k < x ₁, …, х_n > = k_ix_i • k_jx_j • … • k_nx_n }, k_ix_i Î А1_М, k_jx_j Î А2_М, …, k_nx_n Î Аn_М

Например, заданы мультимножества A1_М = {3 a, с }, A2 _М = {2 b, d }, A3_М = {3 e, 2 f }. Тогда их прямое произведение C_M = {18< a, b, e >; 12< a, b, f >; 9< a, d, e >, 6< a, d, f >, 6< c, b, e >, 4< c, b, f >, 3< c, d, e >, 2< c, d, f >}.

Прямой п-ой степенью мультимножества A_М называется прямое произведение n одинаковых мультимножеств A_М:

По аналогии с множествами, для мультимножеств также можно сформулировать некоторые правила выполнения операций:

;

;

;

;

;

A_М + В_М = (A_М È В_М) + (A_М Ç В_М);

A_М D В_М = (A_М È В_М) - (A_М Ç В_М) = ;

(A_М - В_М) Ç (B_М - A_М) = Æ;

A_М È В_М = (A_М + В_М) - (A_М Ç В_М) = (A_М Ç В_М) + (A_М D В_М) = A_М + (B_М - A_М) = B_М + (A_М - В_М);

A_М Ç В_М = (A_М + В_М) - (A_М È В_М) = (A_М È В_М) - (A_М D В_М) = A_М - (A_М - B_М) = B_М - (B_М - A_М);

A_М - В_М = (A_М È В_М) - В_М = A_М - (A_М Ç В_М) = (A_М È В_М) D В_М = A_М D (A_М Ç В_М);

A_М D В_М = (A_М È В_М) - (A_М Ç В_М) = (A_М - B_М) + (B_М - A_М) = (A_М - B_М) È (B_М - A_М) = (A_М + В_М) – 2 • (A_М Ç В_М);

A_М + В_М = (A_М È В_М) + (A_М Ç В_М) = (A_М D В_М) + 2 • (A_М Ç В_М).

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 7.1. Определить мощность и размерность мультимножества A_M:

A_M = {3 a, 7 b, 9 c, 2 d, 4 e, 5 f }.

Решение. Мощность мультимножества A - это общее число экземпляров всех его элементов. Тогда | A | = 30.

Размерность мультимножества - это общее число различных элементов. Тогда /A/ = 6.

 

Пример 7.2. Представьте мультимножество A_M из первого примера в виде гистограммы.

Решение. На рис. 7.1 представлено мультимножество A_M в виде гистограммы. По оси ординат отмечены элементы, а по оси абсцисс - кратность их вхождения в мультимножество.

Рис. 7.1. Представление мультимножества A_M в виде гистограммы

Пример 7.3. Постройте примеры равных, неравных, равномощных и равноразмерных мультимножеств.

Решение. Согласно приведенным выше определениям, мультимножества A_M = {3 a, 3 c, 2 d } и B_M = {3 c, 2 d, 3 a } являются равными.

Мультимножества A_M = {3 a, 2 b, c } и B_M = { a, 3 b, 2 c } являются неравными.

Мультимножества A_M = {3 a, 3 b, 2 c } и B_M = {4 a, 3 b, c } являются равномощными, так как сумма экземпляров элементов этих мультимножеств совпадает и равна 8. Данные мультимножества являются также равноразмерными, так как у них одинаковое общее число различных элементов – 3.

 

Пример 7.4. Примените вышеописанные операции к мультимножествам A_M = {2 a, 6 b, 3 c, d } и B_M = {3 b, 5 c, 2 d, 4 e }.

Решение. Согласно приведенным выше определениям, результат запишется следующим образом:

A_M È B_M = {2 a, 6 b, 5 c, 2 d, 4 e };

A_M Ç B_M = {3 b, 3 c, d };

A_M + B_M = {2 a, 9 b, 8 c, 3 d, 4 e };

A_M - B_M = {2 a, 3 b };

A_M D B_M = {2 a, 3 b, 2 c, d, 4 e };

A_M • B_M = {18 b, 15 c, 2 d };

A_M ´ B_M = {2 a, 6 b, 5 c, 2 d, 4 e }.

 

Пример 7.5. Найдите прямое произведение мультимножеств A_M = {2 a, d } и B_M = {3 b, 5 c }.

Решение. Согласно приведенным выше определениям, результат запишется следующим образом:

A_M ´ B_M = {6< a, b >; 10< a, c >; 3< d, b >, 5< d, c >}.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте понятие мультимножества.

2. Приведите примеры мультимножеств.

3. Дайте формальное определение мультимножества.

4. В чем сходство и различие множества и мультимножества?

5. Что такое мощность и размерность мультимножества? Приведите примеры.

6. Приведите способы сопоставления мультимножеств.

7. Какие мультимножества являются равными, неравными, равномощными, равноразмерными?

8. Опишите операцию объединения мультимножеств.

9. Приведите операцию пересечения мультимножеств.

10. Опишите операцию арифметической суммы и разности мультимножеств.

11. В чем заключается операция прямого произведения мультимножеств?

12. Приведите основные свойства операций над мультимножествами.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1. Определите мощность и размерность следующих мультимножеств: A_M = {3 a, 5 b, c, 8 d, 7 e, 9 f }, B_M = { a, 2 b, 9 c, 4 d, f }, C_M = {2 a, 4 b, 6 c, 3 d, 5 e, 7 f, 9 g }.

2. Представьте мультимножества из задания 1 в виде гистограммы.

3. Определите, являются ли следующие мультимножества равными или неравными.

A_M = {3 a, 5 b, 9 c };

B_M = {5 a, 3 b, 9 c }.

4. Определите, являются ли мультимножества из заданий 1, 3 равномощными или равноразмерными.

5. Выполните операцию объединения мультимножеств из заданий 1, 3.

6. Выполните операцию пересечения мультимножеств из заданий 1, 3.

7. Реализуйте операцию арифметической суммы и разности мультимножеств из задания 3.

8. Реализуйте операцию симметрической разности и дополнения следующих мультимножеств:

A_M = {10 a, 8 b, 6 c, 3 d, 5 e, 7 f, 9 g },

B_M = {2 a, 4 b, 6 c, 9 e, 7 f, 5 g }.

9. Определите прямое произведение следуюших мультимножеств:

A_M = {3 a, 2 b };

B_M = {2 с, 9 d }.

10. Покажите справедливость следующих выражений:

;

;

;

;

для мультимножеств из задания 8.

11. Покажите справедливость следующих выражений:

(A_М - В_М) Ç (B_М - A_М) = Æ;

A_М = (A_М - В_М) + (A_М Ç В_М);

В_М = (B_М - A_М) + (A_М Ç В_М);

A_М È В_М = B_М + (A_М - В_М);

A_М Ç В_М = B_М - (B_М - A_М)

для мультимножеств из задания 8.

 

Возможность многократного вхождения элементов в мультимножество создает новое качество и позволяет расширить класс описываемых, анализируемых и синтезируемых математических объектов.

Часто неясность происходит столько же от многословия, сколько и от излишней краткости.

Ж. Даламбер

8. Нечеткие множества

Понятие нечеткого высказывания, степень истинности нечеткого высказывания, функция принадлежности, операции над нечеткими высказываниями, определение и способы задания нечетких множеств, операции над нечеткими множествами, нечеткие отношения и соответствия

ЦЕЛИ

Освоив эту главу студенты должны:

· иметь понятия о нечетких множествах;

· уметь строить функцию принадлежности;

· определять степень истинности составных высказываний;

· уметь выполнять операции над нечеткими множествами и высказываниями;

· иметь понятие о нечетких отношениях и соответствиях и операциях над ними.

8.1. Нечеткие высказывания

В множествах можно однозначно указать, принадлежит или не принадлежит рассматриваемый элемент данному множеству. Следовательно, рассматриваемые выше множества имеют четкие границы, определяющие принадлежность или не принадлежность элемента множеству. В интеллектуальных системах часто нельзя провести четкую грань между принадлежностью и не принадлежностью элементов множеству. В этой связи возникло предположение описывать множества объектов с расплывчатыми границами принадлежности. Например, как определить понятие красоты, любви, удачи, счастья и других расплывчатых понятий. Л.Заде является основателем теории нечетких множеств. Он предложил ввести числовую меру описания расплывчатых понятий. Это дает возможность использовать существующий математический аппарат для описания, преобразования и исследования расплывчатых понятий.

Пусть задано произвольное непустое множество Х.

Х = {x₁, x₂,..., x_n}. Множество   называется нечетким или расплывчатым множеством в Х и обозначается  = {<m_~А(x), x>}, xÎX.

В нечетком множестве каждый элемент есть кортеж длины два, первая компонента которого обозначается m_~А(х) и называется функцией принадлежности. Она задается на сегменте [0, 1]. Вторая компонента кортежа — элемент множества Х.

При задании множества  каждому элементу х присваивается число 0 £ m_~А(х) £ 1. Это число и определяет степень принадлежности элемента х множеству .

Например, пусть задано некотрое множество X = { x₁, x₂, x₃, x₄ }. Тогда одним из возможных нечетких множеств на множестве Х будет множество  = { < 0.1, x₁ >, < 1, x₂ >, < 0, x₃ >, < 0.8, x₄ >}.

Носителем нечеткого множества  называется подмножество А Í Х, содержащее те элементы из Х, для которых m_~А(х) > 0. Функция принадлежности для каждого нечеткого множества определяется субъективно. В настоящее время для нахождения функции принадлежности используют экспертные системы.

Рассмотрим нечеткие высказывания. Нечетким высказыванием называется предложение, относительно которого можно судить о степени его истинности или ложности.

Например, нечеткое высказывание: “2 — маленькое число”. Данное высказывание является субъективным. Если четкое множество Х на котором выбрано число 2 является – относительно большим, например, |Х|=100. Тогда нечеткое высказывание: “2 — маленькое число” является истинным. Если, например, |Х|=3, тогда рассматриваемое высказывание является ложным.

Нечеткое высказывание, равное 0.5, называется индифферентным, т.к. оно истинно в той же степени, что и ложно. Следовательно истинность нечеткого высказывания является субъективной характеристикой. Нечеткие высказывания бывают простые и составные. Составные образуются из простых с помощью логических операций: отрицания, дизъюнкции, конъюнкции, импликации и эквивалентности.

Отрицанием высказывания  называется нечеткое высказывание не , степень истинности которого определяется по формуле:

                                            ù  = 1 —  .                                    (8.1)

Символ ù в данной главе используется для обозначения инверсии.

Конъюнкцией высказываний ,  называется нечеткое высказывание, степень которого определяется по формуле:

                                         Ù  = min (  Ù ).                       (8.2)

Дизъюнкцией высказываний называется нечеткое высказывание, степень которого определяется по формуле:

                                         Ú  = max (  Ú ).                       (8.3)

Импликацией высказываний называется нечеткое высказывание:

                                      ®  = max (1 — , ).                   (8.4)

Из последнего выражения вытекает, что степень истинности не меньше, чем степень неистинности ее посылки или степень истинности ее следствия.

Эквивалентностью высказываний называется новое составное нечеткое высказывание обозначаемое:

                        «  = min(max(1 - , ),max(1 - , )). (8.5)

Если степени истинности нечетких высказываний  и  одинаковы, то степень истинности эквивалентности лежит в сегменте [0.5, 1].

Пример.

Пусть  = 0.7,  = 0.4, 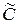 = 0.9 и требуется найти степень истинности следующего составного нечеткого высказывания:

 = (  Ù ù  Ú ù  Ù ) ® ù(  Ù ).

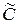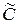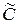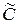 = max(1 — (  Ù ù  Ú ù  Ù ), ù(  Ù )) = = max((1—max(  Ù ù , ù  Ù )), 1 —  Ù ) = = max((1 — max(min(, 1 — ), min(1 — , ))), 1 — min(, )) = max((1 — max(min(0.7, 0.6), min(0.3, 0.4))), 1 — min(0.7, 0.9)) = max(1 — max(0.6, 0.3), 0.3) = max(0.4, 0.3) = 0.4.

При вычислении степени истинности данного составного высказывания использовались формулы (8.1) – (8.5).

Введем понятие степени включения нечетких множеств. Пусть задано множество Х и на нем нечеткие множества , . Тогда степень включения нечеткого множества  в нечеткое множество  обозначается n(, ) и определяется по формуле

n(, ) = Ù (m_~А(х) ® m_~В(х)).

хÎХ

Если n(, ) ³ 0.5, то считается, что нечеткое множество  нестрого включается в .  Í . Если n(, ) < 0.5, то  не включается в .

Например. Пусть на множестве Х = {x₁, x₂, x₃, x₄, x₅} заданы два нечетких множества  = { < 0.3, x₂ >, < 0.7, x₃ >, < 0.9, x₄ > },  = { < 0.1, x₁ >, < 0.8, x₂ >, < 0.3, x₃ >, < 0.9, x₅> }. Тогда степень включения нечеткого множества  в  определяется следующим образом:

n(, ) = (0®0.1) Ù (0.3®0.8) Ù (0.7®0.3) Ù (0.9®0) Ù (0®0.9) = 1 Ù 0.7 Ù 0.7 Ù 1 Ù 1 = 0.7. Следовательно,  Í .

Отметим, что степень включения одного нечеткого множества в другое может быть определена для любых двух нечетких множеств, при этом она может принимать любое значение от 0 до 1.

8.2. Операции над нечеткими множествами

Рассмотрим основные операции над нечеткими множествами.

1) Дано множество Х и на нем заданы нечеткие множества  = { < m_~А(х), x >, xÎX },  = { < m_~B(х), x >, xÎX }.

Объединением нечетких множеств называется выражение вида

 È  = { < m_~АÈ~B(х), x >, xÎX }.

Значение m_~АÈ~B находится согласно следующей формуле:

m_~АÈ~B = m_~А Ú m_~B.

А дизъюнкция находится по формуле (8.3).

Пример. Пусть задано множество Х = { x₁, x₂, x₃, x₄ } и нечеткие множества  = { <0.1, x₁>, <1, x₃> },  = { <0.8, x₁>, <1, x₂>, <0.3, x₃>, <0.7, x₄> }. Тогда их объединение запишется  È  = {<0.8, x₁>, <1, x₂>,<1, x₃>,<0.7, x₄> }.

2)  Ç  — пересечение нечетких множеств, если:

 Ç  = { < m_~АÇ~B(х), x >, xÎX },

m_~АÇ~B = m_~А Ù m_~B

Причем выражение для конъюнкции вычисляется по формуле (8.2).

Пример. Пусть задано множество Х ={x₁,x₂,x₃,x₄} и нечеткие множества  ={<0.1,x₁>,<1,x₃>}, ={<0.8,x₁>, <1,x₂>, <0.3,x₃>, <0.7,x₄>}. Тогда их пересечение запишется Ç  ={< 0.1, x₁>, <0, x₂ >, <0.3, x₃>, <0, x₄>}.

3) Разность.

 \  называется разностью нечетких множеств, если:

 \  = { < m_~А\~B(х), x >, xÎX },

m_~А\~B = m_~А Ù ùm_~B

Согласно формулам (8.1) и (8.2) определяется m_~А\~B.

Пример. Пусть задано множество Х = { x₁, x₂, x₃, x₄ } и нечеткие множества  = { <0.1, x₁>, <1, x₃> },  = { <0.8, x₁>, <1, x₂>, <0.3, x₃>, <0.7, x₄> }. Тогда их разность запишется \  ={<0.1, x₁>,<0, x₂>,<0.7,x₃>,<0,x₄> }.

Симметрической разностью нечетких множеств  и  называется выражение вида

 Q  = { < m_~АQ~B(х), x >, xÎX },

где Q — знак симметрической разности. Выражение для степени принадлежности определяется по формуле

m_~АQ~B = m_~А\~В Ú ùm_~B\~А.

Пример. Пусть задано множество Х = { x₁, x₂, x₃, x₄ } и нечеткие множества  = { < 0.1, x₁ >, < 0.7, x₂ > },  = { < 0.4, x₁ >, < 0.3, x₂ > }. Тогда степень принадлежности для описанных выше операций определятся

а) m_~А\~В(x) = m_~A(x) Ù ùm_~B(x),   

m_~А\~В(x) = { < 0.1, x₁ >, < 0.7, x₂ > };

б) m_~B\~A(x) = m_~B(x) Ù ùm_~A(x),  

ùm_~A(x) = { < 0.9, x₁ >, < 0.3, x₂ > },

 m_~B\~A(x) = { < 0.4, x₁ >, < 0.3, x