Все действия в живой и неживой природе можно описать с помощью алгоритмов

Глава 10. Универсальные алгоритмические модели

Природа устроена рационально, а все явления протекают по точному и неукоснительному плану, который, в конечном счете, является математическим.

Аристотель

Виды универсальных алгоритмов, абстрактный алфавит, числовая функция, машина Тьюринга, графическая схема алгоритма, структурная схема алгоритма, логическая схема алгоритма, алгоритмы Маркова, алгоритмы Ван-Хао, словесное описание алгоритма

ЦЕЛИ

Освоив эту главу, учащиеся должны уметь и знать:

· Строить алгоритмические модели;

· Составлять логическую схему алгоритма;

· Записывать графическую схему алгоритма;

· Составлять структурную схему алгоритма;

· Записывать словесную схему алгоритма;

· Выполнять преобразования на основе алгоритмов Маркова и Ван-Хао.

10.1. Преобразование слов в произвольных абстрактных алфавитах

Существуют три основных типа универсальных алгоритмических моделей:

· преобразование слов в произвольных абстрактных алфавитах;

· преобразование числовых функций;

· представление алгоритмов как некоторого детерминированного устройства, способного выполнять простейшие операции.

В первом типе универсальных алгоритмических моделей под алгоритмом понимают задаваемые соответствия между словами в абстрактных алфавитах (АА). Под абстрактным алфавитом понимается конечная совокупность объектов, называемых буквами или символами этого алфавита. Символами абстрактного алфавита считают буквы, цифры, любые знаки, слова, предложения, любые тексты. Следовательно, абстрактный алфавит — это конечное множество различных символов, и, подобно множеству, его можно задать путем перечисления элементов или символов.

Например, А — абстрактный алфавит: А = { +, а, студент, b, c, учебник }.

Абстрактный алфавит является многоступенчатым, т.е. каждый символ может сам являться алфавитом или его частью. Тогда в соответствии с определением первой алгоритмической модели алгоритмами называют преобразование слов в абстрактном алфавите. Соответственно, словом в абстрактном алфавите называют любую конечную упорядоченную последовательность символов. В качестве примера приведем следующую запись:

Слово А = < +, a >, Слово B = < b, +, c >, Слово C = < >, Слово D = < + >. Здесь слово А состоит из двух символов, В – из трех символов, С – не содержит символов и является пустым, D – содержит один символ.

Число символов в слове абстрактного алфавита называется длиной этого слова.

Алфавитным оператором (АО) называют функцию, которая задает соответствие между словами входного и выходного АА.

Пусть задана система с входным абстрактным алфавитом X и выходным Y. Пусть Х = { a, b, ЭВМ, ПЭВМ }; Y = { a + b, a ´ b, система, ВЦ }. Построим АО, который перерабатывает входные слова алфавита Х в выходные слова алфавита Y. На рис. 2.1 показан один из возможных вариантов алфавитного оператора.

Алфавитные операторы бывают однозначные и многозначные. В однозначном АО каждому входному слову ставится в соответствие одно выходное слово. В многозначных АО каждому входному слову может быть поставлено в соответствие некоторое множество выходных слов. АО, который не ставит в соответствие входному слову никакого выходного, называется неопределенным на этом слове. В примере на рис. 10.1. приведен один из возможных вариантов многозначного АО.

Множество слов, на котором АО определен, называется его областью определения.

Рис. 10.1. Пример алфавитного оператора

Выделяют алфавитные операторы с конечной и бесконечной областями определения. Если область определения АО конечна, то его обычно задают таблицей соответствий. В левой части таблицы записывают слова, входящие в область определения, в правую часть таблицы — слова, получающиеся в результате применения АО к входным словам. Если область определения алфавитного оператора бесконечна, то его задают набором правил, которые за конечное число шагов позволяют найти выходное слово, соответствующее входному.

Алфавитный оператор, задаваемый с помощью конечной системы правил, называется алгоритмом.

Следует различать понятие алгоритма и алфавитного оператора. В АО основное — это соответствие между словами, а не способ его установления. В алгоритме же основное — способ установления соответствия между словами. Следовательно, алгоритм - это АО с правилами, определяющими его действие.

Два алгоритма называются равными, если равны их АО и совпадают системы правил, задающих действие этих алгоритмов на входные слова.

Алгоритмы считаются эквивалентными, если они имеют совпадающие АО, но не совпадающие способы их задания.

Например, пусть алгоритм A1 определяется следующим образом:

X = {a, b, c} – входной абстрактный алфавит;

Y = {a, b, g} – выходной абстрактный алфавит;

Алфавитный оператор (АО1): a ® a, b ® b, c ®g.

Система правил, задающая действие алфавитного оператора: А, В, С.

Пусть алгоритм A2 определяется следующим образом:

X = {a, b, c} – входной абстрактный алфавит;

Y = {a, b, g} – выходной абстрактный алфавит;

Алфавитный оператор (АО2): a ® a, b ® b, c ®g.

Система правил, задающая действие алфавитного оператора: А, В, С.

Тогда алгоритм А1 равен алгоритму А2. Если в алгоритме А2 система правил, задающая действие алфавитного оператора АО2: В, С, А, то алгоритм А1 эквивалентен алгоритму А2.

10.2. Числовые функции

Из определения алгоритма следует, что он ставит в соответствие исходным данным выходные. Поэтому каждому алгоритму можно поставить в соответствие функцию, которую он вычисляет. Рассмотрим теперь второй тип алгоритмических моделей. Их называют числовые функции.

Функцию называют вычислимой, если имеется способ получения ее значений. В алгоритмах часто используются рекурсивные функции, представляющие собой частичный класс вычислимых функций.

Процедуру, которая прямо или косвенно обращается к себе в процессе выполнения алгоритма, называют рекурсивной.

Рекурсия — это способ задания функций, когда ее значения для произвольных значений аргументов выражаются известным образом через значения определяемой функции для меньших значений аргументов.

Алгоритмы, определяющие способы задания рекурсивных функций, часто называют алгоритмами, сопутствующими рекурсивным функциям. Выделяют три способа построения рекурсивных функций: на основе оператора суперпозиции; на основе оператора рекурсии и на основе оператора построения по первому нулю.

Функции, полученные без использования оператора построения по первому нулю, называются примитивно - рекурсивными.

Рекурсивные функции, определенные не для всех возможных значений аргумента, называются частично - рекурсивными.

Рассмотрим рекурсивную функцию (РФ).

В ней различают:

1. Имя, т.е. ее обозначение.

2. Запись (W = f(x₁, x₂, x₃) или F = f(x₁,..., x_n)).

3. Значение функции.

Значение функции отвечает конкретным значениям аргумента. Например, в функции f(x₁, x₂, x₃), аргументы x₁, x₂, x₃ имеют следующие значения x₁ = 1, x₂ = 3, x₃ = 100. Эту же функцию можно эквивалентно представить в следующем виде: f(1, 3, 100).

Рекурсивные функции бывают простые и сложные. Простейшие РФ называют базовыми. Представляющие эти РФ алгоритмы называются одношаговыми. Из базовых РФ на основе операторов можно получать любые составные РФ. Выделяют три типа базовых рекурсивных функций.

1. Функции любого числа независимых переменных, тождественно равные нулю. Их обозначают f₀, j₀.

Если функция записывается в виде j₀ или f₀, то любой совокупности значений аргументов данной функции ставится в соответствие значение ноль. Например, j₀(0) = 0, j₀(3, 5, 7) = 0, j₀(4, 17) = 0.

2. Тождественные функции любого числа независимых переменных вида j_n,i, причем 1 £ i £ n.

Представляющий эту функцию алгоритм запишется: если функциональный знак имеет вид j_n,i, то значением функции следует считать значение (слева направо) i - того независимого переменного. Пример, W = j_3,2(X, Y, Z) = Y, j_3,3(3, 4, 8) = 8. j_3,4(3, 4, 8) = 0 — эта запись не имеет смысла, т.к. n = 3, i = 4 и не выполняется условие 1 £ i £ n. Для тождественных функций n, i ¹ 0.

3. Функции следования.

Представляющий эти функции алгоритм запишется: если функциональный знак имеет вид l, то значением функции следует считать число, непосредственно следующее за числом, являющимся значением алгоритма. Например, операцию получения значения функции следования обозначают “ ‘ ” т.е., 0’ = 1, 1’ = 2... l‘(5) = 6.

Отметим, что базовые функции имеют значения, если заданы значения их аргументов.

Рассмотрим оператор суперпозиции или подстановки. Оператор по функции F от n аргументов и по функциям f1, f2,..., fn строит новую функцию Ф так, что справедливо выражение:

Ф º F(f₁, f₂,..., f_n).

Алгоритм, представляющий данный оператор, запишется: значения функций f₁, f₂,..., f_n принять за значения аргументов функции F и вычислить ее значение.

Пример. Если f₁ = l(y), а F = l(x) и x = l(y), то на основе оператора суперпозиции получится новая функция r(y) = l(l(y)) = l(y’) = y’’. Тогда получили новую функцию r(y) º Ф.

Иногда в алгоритмах вводится знак «::= », что означает «по определению» или «присвоить». Применение этого знака реализует оператор подстановки, который обозначается S.

Например, построение функции Ф из функций F и f_i с помощью оператора суперпозиции можно записать в следующем виде:

Ф::= S[F; f₁, f₂,..., f_n].

Для r(y)::= S[l(x), l(y)].

Рассмотрим оператор рекурсии. Он реализуется на основе двух функций, одна из которых имеет (n-1) независимую переменную, а другая, кроме указанных, еще две, т.е. (n+1).

При этом один из дополнительных аргументов войдет вместе с аргументами первой функции в число аргументов вновь получаемой, а другой, дополнительный, — при выполнении оператора рекурсии.

Оператор рекурсии обозначается R. Его применение записывают в виде следующей строки.

f::= R[f₁, f₂, x(y)], где f — получаемая функция;

f₁ — функция (n-1) независимых переменных;

f₂ — функция (n+1) независимых переменных;

x — главный из дополнительных аргументов;

y — вспомогательный аргумент.

Оператор рекурсии задает функцию с помощью двух условий, в которые входят функции f₁ и f₂.

Например, построение функции предшествования.

f(0) = f₁, f(i’) = f₂(i, f(i)), пр(0) = 0, пр(1) = 0, пр(2) = 1, пр(3) = 2... Здесь пр - это обозначение функции предшествования.

Рассмотрим оператор построения функции по первому нулю. Он по заданной функции, зависящей от (n+1) аргументов, строит новую функцию от n аргументов. Здесь вспомогательный аргумент — исчезает. Например, для функции вида: f::=m [ f₁ (x)], х — исчезающий аргумент.

Тогда алгоритм запишется: придавать вспомогательному аргументу последовательные значения с нуля до тех пор, пока не окажется, что функция f₁ не стала равна нулю (в первый раз). Полученное значение вспомогательного аргумента принять за значение определяемой функции, соответствующее тем значениям основных аргументов, при которых осуществляется описанный процесс.

С помощью перечисленных операторов и функций строится любая сложная функция, которая может представить исследуемый алгоритм.

Сформулируем тезис Чёрча. Какова бы ни была вычислимая неотрицательная целочисленная функция от неотрицательных целочисленных аргументов, всегда существует тождественно равная ей рекурсивная функция.

Тогда тезис Черча можно интерпретировать для анализа алгоритмов следующим образом: каков бы ни был алгоритм, перерабатывающий наборы целых неотрицательных чисел, всегда существует алгоритм, представляющий РФ, который ему эквивалентен.

Тогда реализация алгоритма, в определенном смысле, эквивалентна вычислению значений РФ. При этом невозможность построения РФ будет означать невозможность построения алгоритма.

10.3. Построение алгоритмов по принципу «разделяй и властвуй»

Существует много стандартных приёмов, используемых при построении алгоритмов. Например, сортировка вставками является одним из таких стандартных приемов. При этом алгоритм действует по шагам и происходит последовательное добавление элементов одного за другим к отсортированной части массива. При решении сложных задач большой размерности их часто разбивают на части, определяют решения, а затем из них получают решение всей задачи. Этот прием, если принять его рекурсивно, как правило, приводит к эффективному решению основной задачи, подзадачи которой составляют ее меньшие версии. Этот прием называется принцип «разделяй и властвуй». На основе принципа «разделяй и властвуй» можно построить более быстрый алгоритм сортировки.

Отметим, что многие алгоритмы по природе своей рекурсивны, т.е. решая некоторую задачу, они обращаются сами к себе для решения её подзадач. Идея метода «разделяй и властвуй» состоит как раз в этом. Сначала решаемая задача разбивается на задачи меньшего размера. Затем эти задачи решаются (с помощью рекурсивного вызова - или непосредственно, если размер задачи достаточно мал). Наконец, полученные решения объединяются и получается решение исходной задачи.

Для задачи сортировки процесс решения выглядит так. Сначала массив разбивается на две половины, каждая из которых сортируется отдельно. После чего два упорядоченных массива соединяют в один. Рекурсивное разбиение задачи происходит до тех пор, пока размер массива не станет равным единице (любой массив длины 1 можно считать упорядоченным).

Нетривиальным этапом является объединение двух упорядоченных массивов в один. Оно выполняется с помощью различных вспомогательных процедур.

10.4. Представление алгоритма в виде детерминированного устройства

Математик А. Тьюринг - один из основателей анализа сложности алгоритма. Он разработал идеи представления алгоритмов на основе детерминированных устройств. Такое устройство называется машиной Тьюринга (МТ). Модель машины Тьюринга является третьей алгоритмической моделью. Она состоит из трех частей - ленты, считывающего устройства (головки) и управляющего устройства (УУ) (рис. 10.2).

Рис. 10.2. Представление машины Тьюринга

На рис. 10.2 цифра 1 обозначает ленту МТ. Она представляет собой бесконечную память машины. В качестве ленты можно использовать любой носитель памяти (бумажную или магнитную ленту). Отметим, что лента считается бесконечной длины в обе стороны. Она разбивается на стандартные ячейки одинакового размера. В каждой ячейке может быть записан только один любой символ конечного алфавита. Число возможных символов конечно, и они образуют абстрактный алфавит машины А = {a₁, a₂,..., a_m}. Отсутствие символа в ячейке обозначается специальным «пустым» символом «».

МТ имеет считывающую головку (цифра 2 на рис. 10.2), способную считывать содержимое ячеек. Головка всегда располагается над одной из ячеек ленты. Она может читать и писать символы, стирать их. Лента перемещается вдоль головки в обе стороны таким образом, чтобы в любой момент считывать содержимое одной ячейки ленты. На каждом шаге работы машины головка находится в одном из множества состояний Q = { q₁,..., q_n }, среди которых выделяют начальное q ₁ и конечное q_z, состояния.

Элементарный шаг машины Тьюринга состоит из следующих действий:

· головка считывает символ, записанный в ячейке, над которой она находится;

· считанный символ a_k и текущее состояние головки q_j однозначно определяют новое состояние q_i, новый записываемый символ а_l и перемещение головки d_p (на одну ячейку влево, вправо или остаться на месте).

Кроме этого, МТ имеет устройство управления (УУ), которое в каждый момент находится в одном из состояний Q = { q ₁, q ₂,..., q_n }. Состояние устройства управления называется внутренним состоянием МТ. Одно из состояний является заключительным состоянием МТ и управляет окончанием работы машины. Устройство управления хранит и выполняет команды машины, например, вида q_ja_k → q_ia_ld_p.

Данные в машине Тьюринга — это слова в абстрактном алфавите ленты. На ленте МТ записывают исходные данные и конечные результаты.

Полное состояние машины Тьюринга называется конфигурацией и включает в себя состояние головки, состояние ленты (слово, записанное за ней) и положение головки на ленте. Конфигурация машины Тьюринга описывается тройкой a₁qa₂, где q — текущее состояние головки, а ₁ — слово слева, а а ₂ — слово справа от головки (включая символ, над которым находится головка). Конфигурация, изображенная на рис. 10.2, может быть записана так: а_i «» q_j a_k a_m. Конкретную машину Тьюринга (и алгоритм соответственно) можно задать, перечислив элементы алфавита А, множества состояний Q и команды машины.

Перед началом работы на пустую ленту записывается исходное слово а абстрактного алфавита. Головка устанавливается над первым его символом и, как следствие, начальной конфигурацией является запись вида q₁a.

Работа машины Тьюринга состоит в изменении конфигураций. Конфигурацией машины Тьюринга называется ее полное состояние, по которому можно однозначно определить дальнейшее поведение машины. Оно обозначается тройкой a₁ q_i a₂, где a₁ — слово слева от головки, a₂ — слово, состоящее из символа, просматриваемого головкой и расположенного справа. Стандартной начальной конфигурацией называется конфигурация вида q ₁ a, где просматривается крайний слева символ, записанный на ленте. Стандартной заключительной конфигурацией называется выражение вида q ₂ a. Ко всякой произвольной конфигурации k в машине Тьюринга применима только одна команда типа q_ia_j ® q_i'a_j's_k, которая переводит конфигурацию k в k'.

Совокупность всех команд, которые может выполнять машина Тьюринга, называется программой. При решении задач с входными данными сопоставляется начальная конфигурация k ₀, а выходные данные определяются заключительной конфигурацией, в которую машина Тьюринга переводит k ₀.

Например, рассмотрим машину Тьюринга, переводящую последовательность а ₁, а ₂,..., а_п в последовательность b ₁, b ₂,..., b_п, работающую в соответствии с программой q_ia_j ® q_i'a_j's_k. Считывающая головка, перемещая ленту направо в соответствии с программой, будет стирать символы а ₁, а ₂,..., а_п и вместо них соответственно записывать выходные символы b ₁, b ₂,..., b_п. Если потребовать, чтобы при просмотре клетки ленты с пустым символом машина Тьюринга переходила в заключительное состояние, то после остановки машины на ленте будет выходная последовательность b ₁, b ₂,..., b_п.

Известно, что на машине Тьюринга можно имитировать все алгоритмические процессы, которые можно представить в математическом виде.

А. Тьюринг показал, что если проблемы не могут быть решены на его машине, то они не могут быть решены ни на какой другой автоматической ЭВМ, т.е. это проблемы, для которых алгоритмы не могут быть составлены даже в принципе. Следовательно, невозможность построения машины Тьюринга означает невозможность построения алгоритма решения данной проблемы. Следует отметить, что речь идет об отсутствии алгоритма, решающего всю данную проблему, что не исключает возможности решения этой проблемы в частных случаях различными для каждого случая методами.

10.5. Универсальные схемы алгоритмов

Все операции, выполняемые в алгоритмах, разделяют на две группы: арифметические операции и логические операции. Арифметические операции выполняют непосредственное преобразование информации. Логические операции определяют последовательность выполнения арифметических операций.

Рассмотрим основные универсальные схемы алгоритмов. К ним относят:

· Алгоритмы Ван - Хао.

· Алгоритмы Маркова.

· Алгоритмы Ляпунова.

· Графические схемы алгоритмов (ГСА).

· Структурные схемы алгоритмов (ССА).

· Словесные схемы алгоритмов (СА).

Универсальные схемы алгоритмов Ван - Хао появились в 50-х годах прошлого столетия. Операторный алгоритм Ван-Хао задается последовательностью приказов специального вида. Каждый приказ имеет определенный номер и указание, какую операцию необходимо выполнить над заданным объектом и с каким номером следует далее выполнять действие над результатом этой операции. Например, некоторый приказ записывается следующим образом (рис. 10.3):

i:

w

a

b

Рис. 10.3. Пример приказа

На рис. 10.3 i — номер приказа, w — элементарная операция над заданным объектом, a и b — номера произвольных других приказов. Выполнить приказ i над объектом или числом x означает вычислить w(x) и затем перейти к выполнению над w(x) приказа с номером a, если w(x) не определяется, то перейти к выполнению над числом x приказа с номером b. Заключительному состоянию в алгоритме Ван - Хао соответствует приказ, представленный на рис. 10.4:

i:

стоп

Рис. 10.4. Приказ на окончание работы алгоритма Ван-Хао

Такая запись означает, что вычисления следует прекратить.

В настоящее время схемы алгоритмов Ван-Хао не имеют широкого практического применения, а используются для теоретического представления алгоритмов.

Интерес в практической деятельности представляют нормальные алгоритмы Маркова (НАМ). Они основаны на использовании абстрактных алфавитов и марковских подстановок. В качестве исходных данных и конечных результатов нормальные алгоритмы Маркова (НАМ) используют строки символов, т.е. слова абстрактных алфавитов.

Марковской подстановкой называют операцию над словами, задаваемую парой слов < P, Q >, где P и Q —слова в абстрактном алфавите. Суть подстановки заключается в следующем. В исходном слове С определяется первое вхождение слова Р. Если оно есть, то производится замена этого вхождения словом Q без изменения остальных частей слова С. При этом слова P и Q должны иметь одинаковую размерность.

Пример 10.1. Пусть задано слово С = 832547, и задана пара <P, Q> = <32, 00>. Тогда результатом работы нормального алгоритма Маркова будет слово C’ = 800547.

Пример 10.2. Пусть задано слово С = 832547, и задана пара <P, Q> = <9, 4>). Отметим, что такая марковская подстановка к слову C не применима, так как в нем отсутствует цифра 9.

Нормальные алгоритмы Маркова применяют для анализа и преобразования формульных записей. Тогда НАМ работает следующим образом. Двигаясь по столбцу формул, определяют первую формулу, левая часть которой входит в преобразуемое слово; если такой формулы нет, то процесс окончен. При ее наличии выполняется марковская подстановка, изменяющая преобразуемое слово. После этого проверяется, заключительная ли это подстановка или нет. Если да, то процесс окончен, если нет, то весь процесс повторяется с самого начала.

Например, пусть заданы следующие выражения:

1234567;

9713256;

0001111;

2224444.

И задана пара <P, Q> = <2, B>.

Тогда результат работы НАМ запишется следующим образом:

1В34567;

9713В56;

ВВВ4444.

Нормальные алгоритмы Маркова в основном применяются для преобразования, минимизации и доказательства алгебраических тождеств.

Рассмотрим схемы алгоритмов Ляпунова. Для описания алгоритмов Ляпунова используют логические схемы алгоритмов (ЛСА). Логическими схемами алгоритмов называют выражения, составленные на основе абстрактного алфавита и состоящие из последовательной цепочки операторов и логических условий. В ЛСА операторами являются действия алгоритма, в результате которых происходит обработка и преобразование информации. Операторы обозначают строчными буквами. Прописными буквами в ЛСА обозначают проверяемые логические условия. Последовательность выполнения нескольких операторов представляется в виде их произведения. Операторы в таком предложении выполняются слева направо. После каждого логического условия ставится стрелка вверх (назовем ее условно восходящей), которая обозначает собой переход по условию. Каждая стрелка имеет свой собственный номер. Каждой восходящей стрелке соответствует одна нисходящая (т.е. стрелка вниз) стрелка с тем же номером, что и у восходящей. Таким образом, если заданное логическое условие справедливо, то выполняется следующий оператор, расположенный справа от условного. Если условие ложно - то выполняется оператор, расположенный справа от нисходящей стрелки, имеющей тот же номер.

Приведем пример записи ЛСА:

А₀ ¯¹ A₁ q ­¹ ¯² A₂ p ­² A_k.

Согласно этому выражению работа алгоритма начинается с выполнения левого оператора. Обычно это оператор А₀, представляющий собой начало алгоритма. Затем выполняется следующий справа оператор A₁. Следующий за оператором A₁ оператор q является логическим условием. Поэтому в зависимости от результатов проверки истинности этого условия будут выполняться либо оператор A₂ - если условие q - истинно, либо оператор A₁ (по нисходящей стрелке). Аналогичные действия выполняются и для другого логического условия p. Последним в алгоритме является крайний правый оператор, обозначаемый обычно A_k. Он называется оператором окончания алгоритма.

В общем случае ЛСА Ляпунова должны удовлетворять следующим условиям:

1. Содержать один начальный и один конечный оператор, соответственно А₀ и A_k.

2. Каждому логическому условию должна соответствовать одна стрелка, направленная вверх.

3. Каждому логическому условию всегда соответствует, одна стрелка, направленная вниз.

4. Каждой восходящей (нисходящей) стрелке обязательно соответствует одна нисходящая(восходящая)стрелка.

Пример 10.3. Пусть задана последовательность из n натуральных целых чисел. Составить логическую схему алгоритма нахождения среднего арифметического этих чисел. Тогда данный алгоритм можем записать в виде логической схемы следующего вида:

А₀ ¯¹ A₁ q ­¹ A₂ A₃ ¯² A₄ A₅ p ­² A₆ A₇ A_k,

А₀ – начало алгоритма;

А₁ – ввод исходной последовательности чисел;

q – проверка логического условия: все ли числа введены;

А₂ – задание начального значения для подсчета суммы чисел: S = 0;

А₃ – ввод начального значения переменной цикла: i = 1;

А₄ – суммирование значений чисел последовательности: S = S + x_i;

А₅ – увеличение переменной цикла: i = i + 1;

p – проверка логического условия выхода из цикла: i > n;

А₆ – нахождение среднего арифметического последовательности чисел: D = S / n;

А₇ – вывод найденного значения;

А_k – конец работы алгоритма.

Рассмотрим графические схемы алгоритмов (ГСА). Они представляют собой графическую интерпретацию алгоритмов Ляпунова. Приведем основные правила представления графических схем алгоритмов:

· наличие конечного числа вершин;

· наличие одной начальной и одной конечной вершин;

· входы и выходы вершин соединяются между собой с помощью стрелок, направленных от входа к выходу;

· каждый выход соединяется только с одним входом, каждый вход соединяется, по крайней мере, с одним выходом;

· логическое условие имеет некоторое множество входов, но только два выхода («да», «нет»).

Следовательно, оператор начала А₀ может иметь только выходящие стрелки (рис. 10.5).

Рис. 10.5. Оператор начала ГСА

Оператор преобразования может иметь входящие и выходящие стрелки (рис. 10.6).

Рис. 10.6. Оператор преобразования ГСА

Логическое условие может иметь много входящих стрелок, выходящих стрелок может быть только две (рис. 10.7)

Рис. 10.7. Оператор логического условия

Оператор конца алгоритма имеет только входящие стрелки (рис. 10.8).

Рис. 10.8. Оператор окончания ГСА

Пример 10.4. Пусть задана логическая схема алгоритма следующего вида: А₀¯¹А₁р₁­¹А₂р₂­²А₃¯²А₄А₅А_k. На основе приведенных правил построим эту схему в виде ГСА (рис. 10.9).

Рис. 10.9. Графическая схема алгоритма (ГСА)

Важной разновидностью графического представления алгоритмов являются структурные схемы алгоритмов (ССА). При такой записи алгоритмов происходит как-бы процесс декомпозиции (т.е. расчленения алгоритма на отдельные этапы - блоки). Блоки изображаются графически в виде геометрических фигур. Каждому блоку присваивается собственный номер. Внутри блока в виде формул или словесно записывается информация, характеризующая выполняемые им функции. Блоки соединяются линиями, символизирующими межблочные связи. Блоки могут описывать элементарные шаги алгоритма или представлять собой части алгоритмов или отдельные алгоритмы.

Правила выполнения структурных схем алгоритмов определены ГОСТом 19.701-90 (ИСО 5807-85) “Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения”. Фрагмент текста ГОСТа приведен в приложении. Руководствуясь требованиями данного ГОСТа, можно построить структурную схему алгоритма для решения конкретной задачи.

Пример 10.5. Пусть необходимо построить ССА нахождения минимального числа в заданном множестве чисел.

А = { a ₁, a ₂, a ₃, a ₄}; |A| = 4 = n, a ₁ = 2, a ₂ = 1, a ₃ = 8, a ₄ = 5.

Перед разработкой ССА производится распределение памяти, причем это распределение условное.

Блок «Начало» соответствует началу работы алгоритма.

Блок 1 ввод исходных данных.

Блок 2 задает начальное значение переменной i.

Блок 3 присваивает переменной x значение a_i, причем на первом шаге значение a_i равно a ₁.

Блок 4 сравнивает значение переменной i с n. Это необходимо для определения момента окончания алгоритма.

Блок 5 увеличивает значение переменной i на единицу.

Блок 6 сравнивает предыдущее число a_i с последующим a_i+1.

Блок 7 печатает значение найденного минимального элемента a₂ = 1.

Блок «Конец» соответствует окончанию работы алгоритма.

На рис. 10.10 приведена структурная схема алгоритма.

Рис. 10.10. Пример структурной схемы алгоритма

Пример 10.6. Составить алгоритм определения среднего роста студента учебной группы.

Решение:

1. Область допустимых значений исходных данных определена в самом условии задачи и предполагает, что все обрабатываемые значения могут быть только положительными числами (целыми или дробными, в зависимости от принятой единицы измерения).

2. Математическая модель задачи может быть выражена соотношением

,

где l_i - рост i -го студента, n - число студентов в учебной группе.

6.3. Составляем структурную схему алгоритма. Вариант структурнойсхемы алгоритма для решения этой задачи показан на рис. 10.11.

Рис.10.11. Вариант структурной схемы алгоритма к примеру 6

Следует отметить, что основа структуры алгоритма представляет собой ограниченный набор стандартных способов соединения базовых блоков для выполнения типичных последовательностей действий. Следовательно, любой алгоритм может быть построен на использовании нескольких базовых блоков путемих комбинации друг с другом на основе связок. Такой подход к разработке алгоритмов называется структурным. К связкам относят:

· следование - последовательное размещение блоков или их групп.

· цикл - структура, определяющая выполнение одного и того же действия несколько раз с различными параметрами вычисляемой величины. Циклическая структура предполагает наличие следующих блоков:

а) присваивание, где происходит задание начальных значений параметров вычисляемой величины;

б) тело цикла, представляющего собой последовательность многократно выполняемых действий;

б) условия выполнение цикла, определяющего выполнение действий в теле цикла или прекращение их выполнения.

Различают два типа циклических структур - цикл "с предусловием" (цикл «до») и цикл "с постусловием" (цикл «пока»). Цикл "до" (рис. 10.12, а) позволяет выполнять заданные действия (тело цикла) несколько раз, до тех пор, пока выполняется некоторое условие. Особенность преобразования информации здесь состоит в том, что цикл «до» выполняется всегда (по крайней мере, один раз), т.к. проверка условия выхода из цикла осуществляется только после выполнения действий. Цикл "пока" (рис. 10.12, б) позволяет выполнить заданные действия только после проверки условия. В этом случае цикл"пока", вотличие от цикла "до", может быть не выполнен ни разу;

· разветвление (рис. 10.13) позволяет выполнять, в зависимости от условия, то илииное действие (или группу действий).

· обход (рис.10.14) представляет собой частный случай разветвления, когда при выполнении (или, наоборот, невыполнении) условия никаких действий не выполняется.

    

а) цикл «до»;          б) цикл «пока»

 

Рис. 10.12. Типы циклических структур

Рис. 10.13. Структура разветвления

Рис. 10.14. Структура обхода

Особенность приведенных структурных связок состоит в том, что все они имеют единственные вход и выход. Это позволяет просто и наглядно формировать из них в любой последовательности структуру алгоритма. В этой связи, если принять рассмотренные структурные связки за элементарные алгоритмы, алгоритм любой задачи можно представить следующим образом:

АЛГОРИТМ = {<элементарные алгоритмы>}.

Другими словами, алгоритм состоит из набора элементарных алгоритмов. Приведенное определение алгоритма позволяет при разработке алгоритмов сложных задач использовать иерархический подход. Суть данного подхода состоит в следующем: сначала анализируется и записывается структура алгоритма (при этом в полной мере возможно использование описанных выше структурных связок), а затем детализируются отдельные блоки предложенной структуры. Процесс детализации является итерационным, причем уровень детализации с каждой итерацией повышается. Очевидно, что общая структура алгоритма решения задачи может влиять и влияет на результат программной реализации.

Рассмотрим распространенный способ записи алгоритмов – словесное описание. В этом случае алгоритм задается через описание и перечисление операторов, аналогичных блокам, используемым структурной схемой алгоритма. Таким образом, словесная запись алгоритма представляет собой перечень операторов, пронумерованный в порядке их исполнения алгоритмом. При записи условных операторов помимо указания условия, истинность которого необходимо проверить, указываются также номера операторов, которым будет передаваться управление в зависимости от результатов проверки.

Пример 10.7. Приведем словесное описание структурной схемы алгоритма из примера 5.

1. Присвоить переменной i значение, равное 1.

2. Присвоить х значение, равное a_i (x — произвольная ячейка памяти).

3. Проверяем, i меньше n или нет. Если меньше, то переходим к п.4, иначе переходим к п.6.

4. Переменной i присвоить значение, равное i + 1.

5. Проверка логического условия a_i < x. Если условие выполняется, то переходим к п.2, если нет, то переходим к п.3.

6. Печать минимального числа из множества А.

7. Конец работы алгоритма.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 10.1. Построить логическую схему алгоритма (ЛСА) подсчета арифметического выражения:

.

Решение. Для записи логической схемы алгоритма подсчета данного выражения нами будут использованы следующие операторы:

A₀ - начало программы;

А₁ - ввод объема выборки n;

А₂ - задание начальных значений переменной цикла i = 0 и промежуточной переменной С = 0;

А₃ - оператор увеличения переменной цикла: i = i + 1;

А₄ - вычисление значения индекса переменной b: j = n - i + 1;

А₅ - вычисление значения произведения: p = a_i * b_j;

A₆ - суммирование промежуточных значений p: С = С + p;

q - логический оператор проверки условия: i = n;

А₇ - вычисление значения исходного выражения: у = С / n;

А_k - конец программы.

Ответ: Таким образом, логическая схема алгоритма подсчета данного выражения будет иметь следующий вид:

А₀ А₁ А₂ ¯¹ А₃ А₄ А₅ А₆ q ­¹ А₇ А_k.

Пример 10.2. Построить граф-схему алгоритма (ГСА) подсчета среднего арифметического значения ряда целых четных чисел длины n.

Решение. Графическая схема алгоритма (ГСА) показана на рис. 10.15.

Рис. 10.15. Граф-схема алгоритма

Для построения граф-схемы данного алгоритма используются следующие операторы:

A₀ - начало программы;

А₁ - оператор ввода размера интервала n;

А₂ - оператор ввода начального значения шага: i = 0;

А₃ - наращивание значения шага: i = i + 1;

А₄ - оператор выбора начального числа из заданного интервала а_i;

А₅ - вычисление значения: b = а_i  / 2;

А₆ - вычисление значения: b = b * 2;

p - логический оператор проверки условия: a_i = b;

A₇ - промежуточное суммирование: S = S + a_i;

q - логический оператор проверки условия: i = n;

А₈ - подсчет среднего арифметического: Y = S / 2;

А_k - конец программы.

Пример 10.3. Составить структурную схему алгоритма вычисления 50 значений функции:

Y_i = sin(ax_i)* x_i,

где x_i - это одномерный массив натуральных чисел; i - индекс переменной в массиве: i = 1, 2,..., 50; a - константа.

Решение. Для построения структурной схемы данного алгоритма используем следующие блоки (согласно ГОСТ 19.701-90):

Блок- “НАЧАЛО” - “Терминатор” - неисполняемый блок, символизирующий начало работы алгоритма, всегда располагается перед остальными блоками структурной схемы.

Блок 1 - “Ввод исходных данных” - “Процесс” -в данном блоке осуществляется ввод массива значений переменной x_i и значение константы a.

Блок 2 - “ i = 1 “ - “Процесс” -задает начальное значение индекса переменной.

Блок 3 - “ Y_i = sin(ax_i)* x_i “ - “Процесс” - производится подсчет значения функции Y_i при данном значении переменной x_{i .}

Блок 4 - “Печать значений Y_i и x_i “ - “Процесс” - данный блок задает процедуру вывода на печать значений переменных Y_i и x_{i .}

Блок 5 - “ i = i +1 “ - “Процесс” - увеличивает значение индекса i переменной х на единицу после каждого шага выполнения алгоритма.

Блок 6 - “ i > 50 “ - “Решение” - блок, осуществляющий управление циклом. В случае, если индекс i переменной x меньше или равен 50, т.е. алгоритм подсчитал меньше 50 значений функции Y_i, блок 6 передаст управление блоку 3, таким образом цикл будет повторяться до тех пор, пока не будет произведено 50 вычислений. После этого блок 6 передаст управление следующему по порядку блоку.

Блок- “КОНЕЦ” - “Терминатор” - неисполняемый блок, символизирующий окончание работы алгоритма, всегда располагается после остальных блоков структурной схемы.

Структурная схема алгоритма приведена на рис. 10.16.

Рис. 10.16. Структурная схема алгоритма

Нумерация блоков ведется сверху вниз. В данном примере используется следующий порядок описания блоков: номер блока, затем его название в данной структурной схеме, затем название блока в соответствии с ГОСТом и, наконец, небольшой комментарий к содержанию блока. Стрелки на концах некоторых соединительных линий необходимы, т.к. в соответствии с ГОСТ 19.701 - 90 стандартным считается “направление потока слева направо и сверху вниз”, а в рассматриваемой структурной схеме есть несколько потоков, имеющих нестандартную направленность (например, снизу вверх).

Пример 10.4. Записать словесный алгоритм вычисления выражения, заданного в примере 10.3.

Ответ. Словесная запись алгоритма вычисления исходного выражения будет выглядеть следующим образом:

1. Начало работы алгоритма.

2. Ввод исходных данных.

3. Присвоить i значение 1.

4. Вычислить значение переменной: Y_i = sin(ax_i) / x_i.

5. Вывести на печать значения переменных х_i, Y_i.

6. Присвоить i значение: i + 1.

7. Проверка условия i > 50. Если условие истинно, то перейти к пункту 8 настоящего алгоритма, если условие ложно, то перейти к пункту 4.

8. Конец работы алгоритма.

Пример 10.5. Построить структурную схему алгоритма для подсчета среднего арифметического значения ряда целых четных чисел длины n, заданного в примере 10.2.

Решение: Подробное описание всех блоков структурной схемы алгоритма не приводится, поскольку блоки структурной схемы будут аналогичны операторам граф - схемы алгоритма из примера 10.2. Приведем содержание основных 1-го и 3 -го блоков.

Блок 1 - Ввод размера интервала n и начального значения шага i = 0;

Блок 3 - Выбор начального числа из интервала a;

Ответ. Структурная схема алгоритма показана на рис. 10.17.

 

                                                                              

Рис. 10.17. Пример структурной схемы алгоритма

10.5. “Жадные” алгоритмы

Для решения оптимизационных задач можно использовать класс алгоритмов, называемых “жадными”. В таком алгоритме на каждом шаге делается локально оптимальный выбор, в предположении, что итоговое решение окажется оптимальным. В общем виде, это не верно, но для многих оптимизационных задач такие алгоритмы позволяют получить локальный оптимум, а в частном случае - глобальный оптимум.

Рассмотрим стандартную задачу (Кормен, Лейзерсон, Ривест) о выборе заявок. Пусть даны n заявок на проведение занятий в одной и той же аудитории. Два разных занятия не могут проводиться в одно время. В каждой заявке указаны начало и конец занятия (s_i и f_i для i -той заявки). Разные заявки могут пересекаться, и тогда можно реализовать только одну из них. Каждая заявка отождествляется с промежутком [ s_i, f_i ], так что конец одного занятия может совпадать с началом другого, и это не считается пересечением. Целевая функция задачи заключается в наборе максимального количества совместных друг с другом заявок при временных ограничениях и граничных условиях. Жадный алгоритм работает следующим образом. Предполагаем, что заявки упорядочены в порядке возрастания времени окончания, т.е., f₁ ≤ f₂ ≤ … £ f_n. Заявки с одинаковым временем конца располагаем в произвольном порядке. Тогда запишем псевдокод алгоритма, приведенный в учебнике (Кормен, Лейзерсон, Ривест):

ВЫБОР ЗАЯВОК (s, f - массивы)

1 n ← length [ s ]

2 А ← {1}

3 j ← 1

4 for i ← 2 to n

5 do if s_i ≥ f_j

6 then A ← A È { i }

7 j ← i

8 return A

Множество А состоит из номеров выбранных заявок, j – номер последней из них; при этом f_j = mах{f_k: kÎA}, поскольку заявки отсортированы по возрастанию времени окончания. Вначале А содержит заявку номер 1, и j = 1 (строки 2 - 3). Далее (цикл в строках 4 - 7) ищется заявка, начинающаяся не раньше окончания заявки номер j. Если таковая найдена, она включается в множество А и переменной j присваивается ее номер (строки 6 - 7). Описанный алгоритм выбора заявок требует всего лишь O (n) шагов (не считая предварительной сортировки). Как и подобает жадному алгоритму, на каждом шаге он делает выбор так, чтобы остающееся свободным время было максимально.

Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных (жадных) выборов дает глобально оптимальное решение.

Отметим, что задачи, решаемые с помощью жадных алгоритмов, должны обладать свойством оптимальности для подзадач. А именно, оптимальное решение всей задачи содержит в себе оптимальные решения подзадач.

10.6. Нечеткие (расплывчатые) алгоритмы

Нечеткий (расплывчатый) алгоритм — это упорядоченное множество расплывчатых инструкций, которые при их реализации позволяют получать приближенное решение задач.

Инструкции в расплывчатых алгоритмах делят на три группы.

1-я группа — назначающие инструкции. Например, х = “большой” или х = “вкусный”.

2-я группа — расплывчатые высказывания. Например, если х — “очень дорогой”, то перейти к y, или если х “не помещается в комнате”, то “увеличить размер комнаты”.

3-я группа — безусловные активные предложения. Например, “немного увеличить” х, или “сильно увеличить” х, или перейти к другому значению параметра x.

Отметим, что все инструкции могут быть нечеткими или четкими.

Нечеткие алгоритмы определения — это конечное множество инструкций, определяющих расплывчатое множество в терминах других расплывчатых множеств или дающих метод для определения степени принадлежности каждого элемента для определяемого множества. Алгоритмы идентификации устанавливают степень принадлежности элементов множеству. Алгоритмы порождения используются для порождения новых, а не для определения данных расплывчатых множеств. Примерами таких алгоритмов могут служить алгоритмы сочинения стихов, конструирования ЭВА, разработки технических заданий на изделие. Нечеткиеалгоритмы, используемые для описания поведения произвольной системы, называются бихевиористическими.

Расплывчатой переменной считают кортеж П = < a, X, 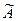>, где a — наименование расплывчатой переменной; X = {x₁, х ₂,..., х_n } — область ее определения; A = {  (x_i) | x_i } x_i Î X — расплывчатое множество в X, определяющее ограничения на возможные значения П. Лингвистической переменной называют кортеж Л = < b, Т, X >, где b — наименование Л; Т — множество ее значений, представляющих наименования П, областью определения которых является X.

Например, пусть оценивается качество технологического процесса выхода годных с помощью понятий “плохой”, “средний”, “хороший”. Максимальный выход годных 80%. Тогда Л = <качество, Т, [0; 80]>, где Т = {“плохой”, “средний”, “хороший”}. Значения Л описываются расплывчатыми переменными. Например, значение “плохой” описывается расплывчатой переменной < плохой, [0; 80], 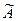 >, где  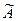может иметь вид  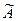= {< 1 / 0 >,
< 0,8 / 5 >,< 0,6 / 7 >,< 0,2 / 20 >}. Значение “хороший” можно, например, описать так: < хороший, [0; 80], 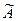>, где  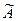= {< 1 / 80 >, < 0,8 / 75 >, <0,6 / 70 >,< 0,2 / 40 >}.

Функцию принадлежности при наличии k экспертов упрощенно определяют так. Пусть k ₁ экспертов на вопрос о принадлежности х Î Х к 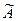 отвечают положительно, а k ₂ = k — k ₁ экспертов на этот же вопрос отвечают отрицательно. Тогда устанавливают следующее значение функции принадлежности:  (x_i) = k ₁ / { k ₁ + k ₂). Для точных оценок приводят парные сравнения функций принадлежности и др. Лингвистические переменные используют для построения расплывчатых моделей и алгоритмов.

Например, приведем нечеткий алгоритм. Пусть у — быстродействие системы, состоящей из двух ЭВМ, а х — быстродействие одной ЭВМ в системе.

Тогда запишем следующий нечеткий алгоритм построения системы с заданным быстродействием:

1°. Если х “мало” и х “незначительно увеличить”, то у “незначительно увеличится”.

2°. Если х “мало” и х “значительно увеличить”, то у “увеличится значительно”.

3°. Если х “велико” и х “увеличить значительно”, то у “увеличится очень значительно”.

Заметим, что значения расплывчатых условных предложений в этом алгоритме можно определить, если даны значения первичных терминов «большой», «маленький» и расплывчатых терминов «незначительно», «значительно», «очень значительно». Значения указанных терминов субъективны и зависят от носителя нечеткого множества. Например, если четкое множество X = {1, 2, 3, …, 10}, то при x = 9 мы имеем, скорее всего, термин «большой». Если четкое множество X = {1, 2, 3, …, 1000}, то при x = 9 мы имеем, скорее всего, термин «маленький».

Нечеткий алгоритм, который служит для получения приближенного описания стратегии и решающего правила, называется нечетким алгоритмом принятия решений. К такому классу можно отнести алгоритмы принятия решений при пересечении перекрестка, компоновке кристаллов интегральной микросхемы, определении жизненного цикл изделий и др. На рис. 10.18 приведена структурная схема нечеткого алгоритма трассировки (определения путей между частями интегральной схемы).

Рис. 10.18. Структурная схема нечеткого алгоритма «Трассировка»

Эту структурную схему (рис. 10.18) можно представить в виде следующих нечетких инструкций:

1°. Сделать шаг трассировки. Если не трассируется “большое” число связей, то перейти к 1°.

2°. Если не трассируется “небольшое” число связей, то сделать “малый” шаг и перейти к 2°.

3°. Если не трассируется “очень маленькое” число связей, то сделать “очень маленький шаг” и перейти к 3°.

4°. Конец работы алгоритма.

Рассмотрим пример размещения БИС на подложке. Структурная схема одного из возможных алгоритмов такого типа показана на рис. 10.19. В терминах нечетких высказываний структурная схема алгоритма может быть переведена в расплывчатые инструкции.

Рис. 10.19. Структурная схема расплывчатого алгоритма размещения

Следует отметить, что конструктор хорошо оперирует расплывчатыми понятиями «большое», «маленькое», «очень маленькое» и эффективно реализует данный алгоритм в интерактивном режиме связи с ЭВМ. При определении степени принадлежности можно формализовать алгоритм и реализовать его на ЭВМ. Отметим, что операция «сделать шаг» в алгоритме (рис. 10.18) может быть сложным алгоритмом перетрассировки всего кристалла или небольшой его области, или простого удаления нескольких трасс и т.п. Реальные варианты нечетких алгоритмов представляют сложную структуру и необходимо разбиение его на части меньшей размерности. Важным в разработке и применении таких алгоритмов является то, что они могут служить эффективным сред