Идея операторного метода заключается в сведении системы дифференциальных уравнений Кирхгофа относительно переходных токов и напряжений, как функций времени, называемых оригиналами к системе алгебраических уравнений относительно изображений токов и напряжений, как функций комплексной переменной 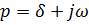 . Такой переход осуществляется методами операционного исчисления (с помощью интегральных преобразований) линейные дифференциальные уравнения с постоянными коэффициентами преобразуются в алгебраические уравнения. Это позволяет не только упростить расчёт переходных процессов, но и унифицировать расчёт электрических цепей, т.е. цепи постоянного тока, цепи переменного синусоидального тока и переходные процессы рассчитываются одними и теми же методами (правда, при этом вычисления выполняются с разными числами: действительными в цепях постоянного тока, комплексными в цепях синусоидального тока, полиномами (степенными многочленами) комплексной переменной p в случае переходных процессов). В электротехнике обычно используются интегральное преобразование Лапласа (или близкое к нему преобразование Карсона).
. Такой переход осуществляется методами операционного исчисления (с помощью интегральных преобразований) линейные дифференциальные уравнения с постоянными коэффициентами преобразуются в алгебраические уравнения. Это позволяет не только упростить расчёт переходных процессов, но и унифицировать расчёт электрических цепей, т.е. цепи постоянного тока, цепи переменного синусоидального тока и переходные процессы рассчитываются одними и теми же методами (правда, при этом вычисления выполняются с разными числами: действительными в цепях постоянного тока, комплексными в цепях синусоидального тока, полиномами (степенными многочленами) комплексной переменной p в случае переходных процессов). В электротехнике обычно используются интегральное преобразование Лапласа (или близкое к нему преобразование Карсона).
Изображением функции действительной переменной i(t) называют функцию комплексной переменной p, которая ставится в соответствие функции i(t) с помощью интеграла Лапласа:
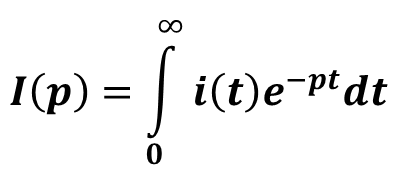
В электротехнике функцию I(p) называют операторным током. Соответствие между изображением I(p) и его оригиналом i(t), или соответствие между операторным током I(p) и переходным током i(t) коротко записывается в виде

Первое из этих соотношений читается как изображение (операторный ток) I(p) соответствует оригиналу (переходному току) i(t); второе – как оригинал (переходный ток) i(t) имеет изображение I(p), или переходному току соответствует операторный ток I(p).
Определения операторного напряжения и операторной ЭДС аналогичны определению операторного тока.
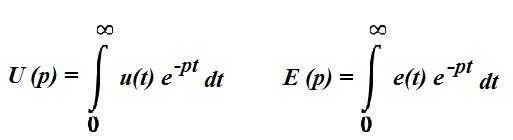
Некоторые свойства преобразования Лапласа
Напомним ряд элементарных свойств преобразования Лапласа, которые будут использоваться в последующем:
- изображение суммы функций времени равно сумме изображений этих функций. Точнее, если 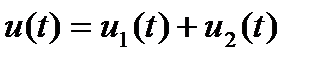 и найдены изображения
и найдены изображения 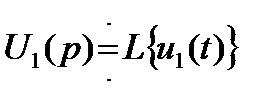 и
и 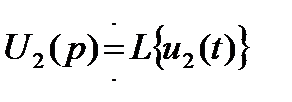 ,то изображение U(p) функции u(t) равно
,то изображение U(p) функции u(t) равно
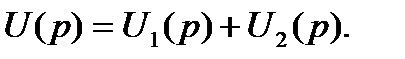
Количество слагаемых в сумме может быть любым, и она является в общем случае алгебраической суммой.
- изображение функции времени, умноженной на постоянную, равно изображению этой функции, умноженную на ту же постоянную. Иначе говоря, если 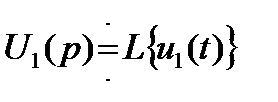 и
и 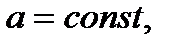 то
то 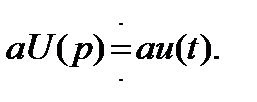
Интегральное преобразование Лапласа является линейным преобразованием и преобразует линейную комбинацию функций времени в линейную комбинацию их изображений с теми же коэффициентами.
Важнейшим свойством преобразования Лапласа является то, что оно переводит производные и первообразные (интегралы с переменным верхним пределом) в алгебраические выражения для изображений.
Изображение производной функции времени равно изображению этой функции, умноженному на p, с вычетом начального значения. На языке формул,
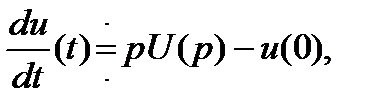
Изображение интеграла с переменным верхним пределом от функции времени равно изображению подынтегральной функции, деленному на p, т.е.
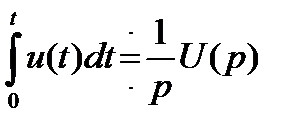
Приведем еще для справки изображения нескольких функций времени, часто встречающихся в электротехнике.
Изображение экспоненциальной функции
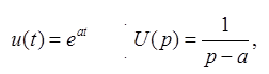
Если в последней формуле положить a=0, то получится, что 
 .
.
Получаем, что изображение постоянной есть та же постоянная, деленная на p:
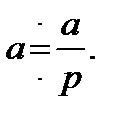
Изображение тригонометрических функций
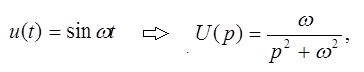
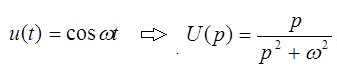 .
.
Учитывая свойства преобразования получим изображения напряжений на индуктивности и емкости в ЭЦ.
С учетом свойств преобразования Лапласа для идуктивности связь между оригиналами тока и напряжения и между их изображениями имеет вид
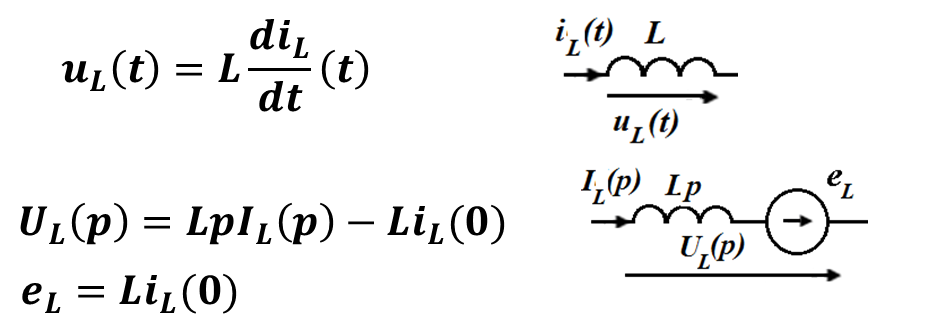
Здесь же изображены схемные представления элемента индуктивность со стрелками токов и напряжений для оригиналов и изображений по Лапласу. Схемное представления элемента индуктивность для изображений по Лапласу называется операторной схемой замещения. Как видно, в операторной схеме индуктивности появился источник эдс, определяемый током в индуктианости в момент коммутации и направление стрелки этого источника совпадает с направлением тока в индуктивности.
Для элемента емкость аналогичные преобразования дают следующие связи и схемы:
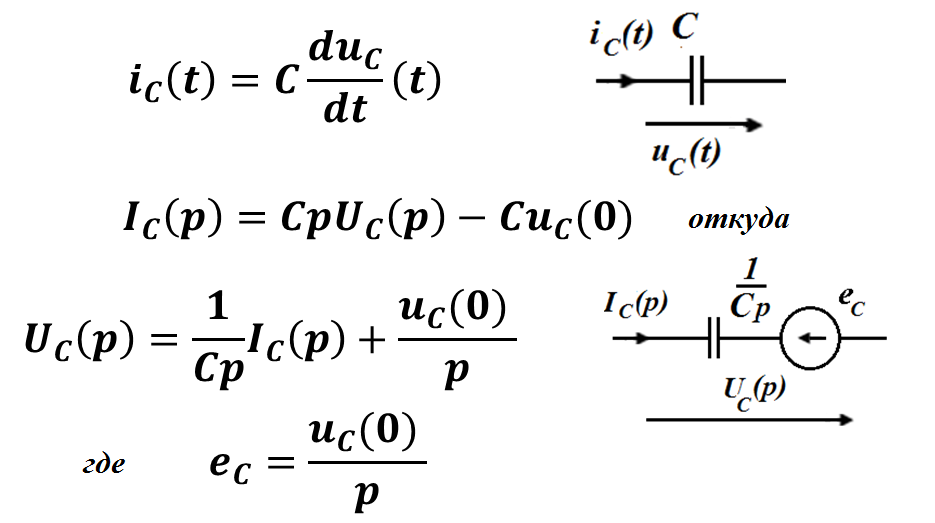
Дополнительный источник эдс в операторной схеие емкости определяется напряжением на емкости в момент коммутации и его стрелка противоположна стрелке тока.
В операторных схемах замещения индуктивности и емкости появляются операторные сопротивления вместо элементов индуктивность и емкость в схемах оригиналов.

Таким образом функциональное преобразование Лапласа переводит уравнения Кирхгофа и закон Ома изобдасти оригиналов в операторную форму.
Закон Ома

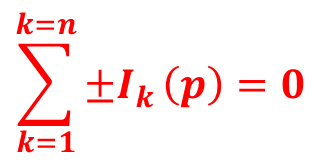
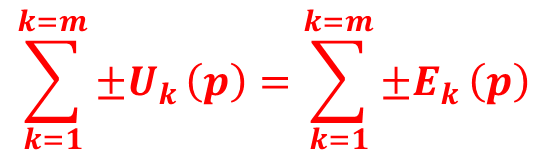
Получившаяся система алгебраических уравнений Кирхгофа относительно изображений токов и напряжений позволяет получить операторное выражение для переходного тока или напряжения. При этом для расчета операторных токов в цепи можно использовать все методы применяемые в цепях постоянного и синусоидального тока, а именно, универсальный метод (по законам Кирхгофа), метод контурных токов, метод узловых потенциалов, метод эквиавалентного генератора, метод наложения, метод эквивалентных преобразований. В отличии от цепей постоянного и синусоидального тока, где результатом расчета являются действительные и комплексные числа, получающиеся операторные токи являются функциями комплексной перемнной p
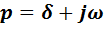
Чтобы вернутся от изображения к оригиналу(то есть функции времени) следует воспользоваться либо таблицами соответствия (в математических справочниках), либо теоремой разложения.
Теорема разложения
Операторное изображение тока, полученное в результате расчета операторной схемы, с помощью обратного преобразования Лапласа позволяет получить оригинал тока как функцию времени. Из математической теории операционного исчисления следует, что операторное изображение тока представляет из себя отношение двух полиномов.
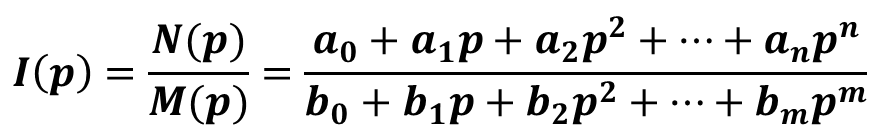
При этом степень полинома знаменателя больше степени полинома числителя 
Известно, что такое алгеабрическое выражение может быть представлено в вид суммы простейших дробей
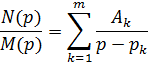
где pk корни полинома знаменателя
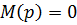
Каждая простая дробь в соответствии с преобразованием Лапласа в оригинале соответствует экспоненциальной функции времени
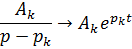
Коэффециенты простых дробей 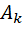 определяются по известным формулам
определяются по известным формулам
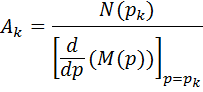
Таким образом оригинал переходного тока можно определить по теореме разложения
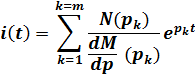
 2020-04-07
2020-04-07 921
921








