Простейшие интегральные уравнения

Интегральное исчисление тесно связано с дифференциальным исчислением. Центральными понятиямиинтегрального исчисления являются понятия определенного интеграла и неопределенного интеграла функций одной действительной переменной.

Определенный интеграл используется для решения задач об измерении площадей, ограниченных кривыми, длин дуг кривых, площадей поверхностей тел, объемов тел, а также задач определения координат центров тяжести, моментов инерции, пути тела по известной скорости движения, работы, производимой силой и многие другие задачи естествознания и техники.

Геометрически определенный интеграл представляет собой сумму площадей S_n, прямоугольников, встроенных в площадь S, ограниченную криволинейной границей. Сумма площадей прямоугольников S_n рассматривается в качестве приближения к полной площади S

, (2.18)

где — символ суммы (греческая буква «сигма»);

— некоторая точка отрезка абсциссы.

Выражение (2.18) для общей площади тем точнее, чем меньше длина участков разбиения. Для нахождения точного значения площади S надо найти предел сумм S_n в предположении, что число точек деления неограниченно увеличивается и наибольшая из длин стремиться к нулю.

Отвлекаясь от геометрического содержания рассматриваемой задачи, приходим к понятию определенного интеграла от функции 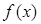, непрерывной на отрезке , в виде предела суммы S_n при том же предельном переходе. Этот интеграл обозначается .

Символ (удлиненное S — первая буква слова Summa) называется знаком интеграла, — подынтегральной функцией, числа a и b называются нижним и верхним пределами определенного интеграла.

Свойства определенного интеграла:

— если a=b, то, по определению, полагают

(2.19)

— если пределы перемещаются

(2.20)

— интеграл суммы (разности) равен сумме (разности) интегралов

(2.21)

— интеграл с постоянной величиной k

(2.22)

— численное значение интеграла не зависит от выбора обозначения переменной интегрирования

. (2.23)

Интегралы геометрических фигур имеют вид:

— длина дуги плоской кривой заданной уравнением

(2.24)

— объем тела, образованного вращением этой дуги вокруг оси OХ

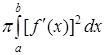(2.25)

— площадь поверхности этого тела

. (2.26)

Фактически вычисление определенных интегралов осуществляется различными способами: в виде предела интегральной суммы, приближенное вычисление по квадратурным формулам, с помощью ЭВМ, графические методы и др.

Неопределенный интеграл не имеет пределов, т. е. они неизвестны. Нахождение этого рода интегралов, или интегрирование, есть операция обратная дифференцированию. При дифференцировании данной функции находят ее производную. При интегрировании, наоборот, находят первообразную (или примитивную) функцию – такую функция, производная которой равна подинтегральной функции. Таким образом, функция F(x) является первообразной для данной функции если или, что тоже самое, . 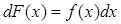Данная функция может иметь различные первообразные, но все они отличаются друг от друга только постоянными слагаемыми с. Поэтому все первообразные для содержатся в выражении , которое называют определенным интегралом от функции 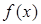и записывают в виде

. (2.27)

Взаимно обратный характер операций интегрирования и дифференцирования выражается равенствами:

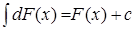. (2.28)

Для упрощения использования неопределенных интегралов имеется таблица основных (табличных) интегралов и правил интегрирования (приложение Б).

Продемонстрируем использование метода простейших интегральных уравнений нижеследующим примером.

Пример 2.3

Найти закон прямолинейного движения материальной точки массой m, если известно, что работа действующей на точку силы пропорциональна времени τ, прошедшему от начала движения. Начальный путь и начальная скорость материальной точки равны соответственно и .

Из курса механики известно, что в случае прямолинейного перемещения точки, когда направляющая силы и скорости совпадают, работа 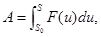где F (u) — сила, действующая на точку.

По условию задачи . Сравнивая оба выражения, находим .

Дифференцируем по S и получаем или Так как – скорость движения, а то С другой стороны, из второго закона Ньютона следует, что 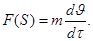Сравнивая оба выражения, имеем . Разделяя переменные и интегрируя, получаем Общее решение этого уравнения представляется в виде

При выполнении условия и имеем Следовательно Заменяя на и интегрируя как сложную функцию, имеем При и получаем С учетом этого выражения закон движения материальной точки принимает вид