ЛЕКЦИЯ 18.03.2020 для гр. КТПм-19-о
ТЕМА: Понятие дифференциального исчисления. Уравнение в дифференциалах. Дифференциальные уравнения в производных. Простейшие интегральные уравнения.
Понятие дифференциального исчисления
Дифференциальное исчисление — раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление дифференциального исчисления в самостоятельную математическую дисциплину связано с именами И. Ньютона и Г. Лейбница (вторая половина 17 в.). Они сформулировали основные положения дифференциального исчисления и указали на взаимно-обратный характер операций дифференцирования и интегрирования. Аппаратом дифференциального исчисления служат центральные понятия производная и дифференциал.
Понятие производной удобно объяснять на решении геометрической задачи построения касательной к плоской кривой в некоторой ее точке М (рисунок 2.6).

Рисунок 2.6 — Геометрическая интерпретация производной
Пусть кривая Г есть график функции 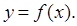 Положение касательной будет определено, если найдется ее угловой коэффициент, т. е. тангенс угла
Положение касательной будет определено, если найдется ее угловой коэффициент, т. е. тангенс угла  , образованного касательной с осью OX. Обозначив через
, образованного касательной с осью OX. Обозначив через  абсциссу точки М, а через
абсциссу точки М, а через  – абсциссу точки
– абсциссу точки 
 . Угловой коэффициент секущей
. Угловой коэффициент секущей 
 равен
равен
 ,
,
где  — приращение функции на отрезке
— приращение функции на отрезке  .
.
Определяя касательную в точке М как предельное положение секущей  , когда
, когда  стремится к
стремится к 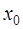 , получаем
, получаем
 . (2.13)
. (2.13)
Производной функции  в точке
в точке  называется предел, (если он существует) отношения приращения функции к приращению аргумента, когда последнее стремится к нулю так, что
называется предел, (если он существует) отношения приращения функции к приращению аргумента, когда последнее стремится к нулю так, что
 . (2.14)
. (2.14)
С помощью производной определяется ряд важных понятий естествознания.
Производную функции  обозначают
обозначают 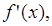
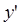 ,
,  или Df (x). Операцию нахождения производной называют дифференцированием. На классе функций, имеющих производную, эта операция линейна.
или Df (x). Операцию нахождения производной называют дифференцированием. На классе функций, имеющих производную, эта операция линейна.
Если производная 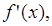 в свою очередь, имеем производную, то ее называют второй производной функции
в свою очередь, имеем производную, то ее называют второй производной функции 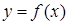 и обозначают
и обозначают  ,
,  ,
,  (произносят де квадрат игрек по де икс дважды) или
(произносят де квадрат игрек по де икс дважды) или  . Для прямолинейного движения точки вторая производная характеризует ее ускорение. Аналогично определяются и производные более высокого порядка. Производная порядка n обозначается
. Для прямолинейного движения точки вторая производная характеризует ее ускорение. Аналогично определяются и производные более высокого порядка. Производная порядка n обозначается  или
или  .
.
В приложении А дается таблица дифференцирования.
Дифференциал функции 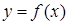 обозначается
обозначается  или
или  . Функция
. Функция 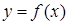 , область определения которой содержит некоторую окрестность точки
, область определения которой содержит некоторую окрестность точки  , называется дифференцируемой в точке
, называется дифференцируемой в точке  , если приращение
, если приращение 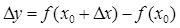 можно записать в форме
можно записать в форме  , где
, где 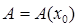 ,
,  при
при  . В этом и только в этом случае выражение
. В этом и только в этом случае выражение  называется дифференциалом функции f(x) в точке
называется дифференциалом функции f(x) в точке  . Геометрически дифференциал (при фиксированном значении
. Геометрически дифференциал (при фиксированном значении  и изменяющемся приращении
и изменяющемся приращении  ) изображает приращение ординаты касательной, т. е. отрезок NT. Дифференциал dy представляет собой функцию, как от переменной х, так и от ее приращения
) изображает приращение ординаты касательной, т. е. отрезок NT. Дифференциал dy представляет собой функцию, как от переменной х, так и от ее приращения  . При фиксированном
. При фиксированном  , dy есть линейная функция от
, dy есть линейная функция от  и разность
и разность  есть бесконечно малая относительно
есть бесконечно малая относительно  . Для функции
. Для функции  имеем,
имеем, 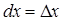 т. е. дифференциал независимой переменной совпадает с его приращением. Поэтому обычно пишут
т. е. дифференциал независимой переменной совпадает с его приращением. Поэтому обычно пишут  . Имеется тесная связь между дифференциалом функции и ее производной и поэтому справедливо равенство
. Имеется тесная связь между дифференциалом функции и ее производной и поэтому справедливо равенство  . Правила нахождения дифференциалов непосредственно вытекает из соответствующих правил нахождения производных. Рассматриваются также дифференциалы высших порядков. На практике с помощью дифференциалов часто выполняют приближенные вычисления значения функций, а также оценивают погрешности вычислений. Пусть, например, надо вычислить значение функции f(x 1 )
. Правила нахождения дифференциалов непосредственно вытекает из соответствующих правил нахождения производных. Рассматриваются также дифференциалы высших порядков. На практике с помощью дифференциалов часто выполняют приближенные вычисления значения функций, а также оценивают погрешности вычислений. Пусть, например, надо вычислить значение функции f(x 1 )  в точке x 1, если известно значение в точке x 0 и
в точке x 1, если известно значение в точке x 0 и  . Заменяя приращении функции ее дифференциалом, получают приближенное равенство
. Заменяя приращении функции ее дифференциалом, получают приближенное равенство

Погрешность этого равенства приближенно равна половине второго дифференциала функции, т. е.
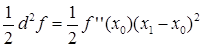 . (2.15)
. (2.15)
 2020-04-12
2020-04-12 174
174







