2020-04-12
110
Для составления дифференциальных уравнений используется видоизмененный метод дифференциалов, который называется «метод производных». Сущность метода производных заключается в том, что из условия задачи составляются приближенные соотношения между скоростями изменения функции Y и аргумента X. Вообще мера скорости применена к разнообразным исследуемым процессам и физическим величинам, что позволяет составлять математические модели в форме дифференциальных уравнений в производных.
Например, сила электрического тока определяется как предел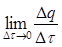 
, где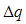 
— положительный электрический заряд, переносимый через сечение цепи за время 
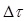. Или скорость химической реакции определяется как предел 
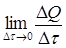, где 
— изменение количества вещества за время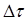 
.
Пример 2.2
Продемонстрируем метод производных на экологическом примере размножения особей простейших одноклеточных бактерий или дрожжей. Скорость прироста популяции равна 
. Она пропорциональна числу особей 
Можем записать простое линейное дифференциальное уравнение.
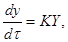(2.16)
где k — коэффициент пропорциональности и размерности, в нашем случае параметр размножения. Разделяем переменные и интегрируем выражение (2.16) 
Уравнение получаем 
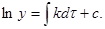Потенциируя, находим 
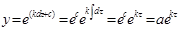, где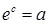 
— постоянная, характеризующая некоторое начальное число особей.
Окончательная формула размножения особей популяции имеет вид
(2.17)
