Уравнение в дифференциалах

При составлении дифференциальных уравнений первого порядка удобно применять «метод дифференциалов». Пусть дана функция . Приращение аргумента  вызывает приращение функции , что можно записать . Поскольку область определения функции 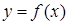 содержит некоторую окрестность точки , то, как показано в 2.5,  или в иной форме где

При фиксированном 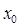,  есть линейная функция от  и разность  есть бесконечно малая относительно . На этом основании малые приращения величин  заменяют их дифференциалами 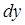, при этом неравномерно протекающие процессы в течение малого промежутка времени  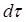 рассматриваются как равномерные. Рассмотрим метод дифференциалов на геометрическом примере.

Пример 2.1

Требуется определить форму поверхности, по которой нужно отшлифовать зеркало рефлектора, чтобы выходящие из одной точки световые лучи после отражения в зеркале пересекались в другой точке. Задача сводится к нахождению уравнения сечения, поверхности меридианной плоскостью, проходящей через точку , в которой помещен источник света, и точку 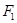, в которой пересекаются отраженные лучи. Как показано на рисунке 2.7

Рисунок 2.7 — Схема лучей к составлению дифференциального уравнения сечения зеркальной поверхности рефлектора

Из точек  и 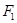 как из центров проведем дуги окружностей c радиусами  и  соответственно. В силу малости MN, QN, MQ будем считать прямолинейными отрезками. Треугольники MQN и MQP прямоугольные и равнобедренные с общей гипотенузой MQ. Поэтому QN=  и . Эти приращения должны быть сошлифованы по пунктирной линии. Заменяя приращения радиусов-векторов  и  их дифференциалами имеем дифференциальное уравнение  Перепишем его следующим образом =d0 и проинтегрируем . Откуда получим , где С постоянная величина. Последнее выражение есть уравнение эллипса. Следовательно, зеркало рефлектора надо шлифовать по поверхности эллипсоида вращения.