2020-04-12
93
Розглянемо неоднорідне диференціальне рівняння
(91)
де р, q — задані дійсні числа, f(х) ≠ 0 — задана функція, неперервна на деякому проміжку (а, b).
Згідно з теоремою п. 3.3, загальний розв'язок такого рівняння являє собою суму частинного розв'язку рівняння (91) і загального розв'язку відповідного однорідного рівняння. Загальний розв'язок однорідного рівняння ми вже знаходити вміємо, тому розглянемо детальніше питання про знаходження частинного розв'язку неоднорідного рівняння.
Насамперед слід зазначити, що частинний розв'язок неоднорідного диференціального рівняння (91) можна знайти в квадратурах методом варіації довільних сталих (п. 3.4). Проте для рівнянь із спеціальною правою частиною частинний розв'язок можна знайти значно простіше, не вдаючись до операції інтегрування.
Розглянемо деякі з таких рівнянь.
І. Нехай права частина в рівнянні (91) має вигляд
(92)
де 
— дійсне число, Рn(х) — многочлен степеня n. Можливі такі випадки:
а) число не є коренем характеристичного рівняння
|
|
|
(93)
Тоді диференціальне рівняння (91) має частинний розв'язок виду
, (94)
де А0, Al,., Аn — невизначені коефіцієнти.
Справді, підставляючи функцію (94) в рівняння (91), після скорочення на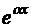 
дістанемо
(95)
де 
— многочлен степеня n - 2, 
— многочлен степеня n — 1, a 
і 
— многочлени степеня n. Таким чином, зліва і справа в тотожності (95) стоять могочлени степеня n. Прирівнюючи коефіцієнти при однакових степенях n, дістанемо систему n + лінійних алгебраїчних рівнянь, з якої визначимо n + 1 невідомих коефіцієнтів Aі многочлена .
Не зупиняючись далі на доведеннях (див. [24]), вкажемо форму, в якій потрібно шукати частинний розв'язок рівняння (91), залежно від виду правої частини 
цього рівняння;
б) якщо число збігається з одним коренем характеристичного рівняння (93), тобто є простим коренем цього рівняння, то частинний розв'язок рівняння (91) треба шукати у вигляді
(96)
в) якщо число є двократним коренем рівняння (93), то частинний розв'язок рівняння (91) шукають у вигляді
(97)
Об'єднаємо випадки а) — в): якщо права частина рівняння (91) має вигляд (92), то частинний розв'язок цього рівняння треба шукати у вигляді
де — многочлен з невизначеними коефіцієнтами того самого степеня, що й многочлен , а г — число коренів характеристичного рівняння, які дорівнюють . Якщо не є коренем характеристичного рівняння, то приймаємо г = 0.
II. Нехай права частина в рівнянні (91) має вигляд
, (98)
де — многочлен степеня n, Rm(х) — многочлен степеня m; та 
— дійсні числа. (Функція (92) є окремим випадком функції (98) і утворюється з неї при = 0).
Частинний розв'язок рівняння (91) треба шукати у вигляді
, (99)
|
|
|
де Qs(х) та Ls(х) — многочлени степеня s з невизначеними коефіцієнтами; s — найвищий степінь многочленів Rm(х) та , тобто s = max (n, m); г — число коренів характеристичного рівняння, які дорівнюють + і.
Зокрема, якщо права частина рівняння (91) має вигляд
f(x) = A cos x + B sin x, (100)
де А, В — відомі дійсні числа, то частинний розв'язок цього рівняння треба шукати у вигляді
(101)
де a, b - невідомі коефіцієнти; г - число коренів характеристичного рівняння (93), які дорівнюють і.
Зауваження. 1. Шукані многочлени у формулах (94), (96) і (97) мають бути повними, тобто містити всі степені х від 0 до n, незалежно від того, чи повним є заданий многочлен . Те саме стосується многочленів QS(x) та LS(x) у формулі (99), причому невизначені коефіцієнти при одних і тих же степенях х у цих многочленах повинні бути, взагалі кажучи, різними.
Зауваження 2. Якщо права частина рівняння (91) є сумою декількох різних за структурою функцій виду (92) або (98), то для відшукання частинного розв'язку потрібно використати теорему про накладання розв'язків (п. 3.4).
Зауваження 3. Використаний метод підбору окремого частинного розв'язку рівняння (91) можна застосовувати лише для певних диференціальних рівнянь, а саме для лінійних рівнянь із сталими коефіцієнтами І з спеціальною правою частиною виду (92) або (98). В інших випадках частинний розв'язок треба шукати методом варіації довільних сталих.
