Ймовірність – числова характеристика появи випадкової події за певної умови, яка може бути відтворена необмежену кількість разів.
Означення: Ймовірністю випадкової події називають відношення кількості наслідків випробувань, які сприяють появі цієї події, до загальної кількості всіх рівно можливих несумісних наслідків, які утворюють повну групу подій.
Позначають  , де n – загальна кількість всіх рівно можливих результатів експерименту; m – кількість результатів експерименту, сприятливих для події А.
, де n – загальна кількість всіх рівно можливих результатів експерименту; m – кількість результатів експерименту, сприятливих для події А.
Розглянуте означення ймовірності називають класичним. Із нього випливають такі властивості:
1) Ймовірність кожної події А є невідיємним числом, що не перевищує одиниці. Справді, число m випробувань, сприятливих для події А, справджує нерівності  , звідки
, звідки  , тобто
, тобто  .
.
2) Ймовірність неможливої події Ø дорівнює нулю: Р(Ø)=0. дійсно, за формулою  .
.
3) Р(Ω)=1, (нормування).
4) 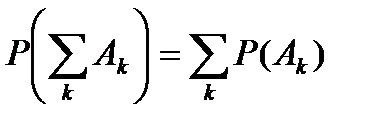 , (повна адитивність для повної групи подій).
, (повна адитивність для повної групи подій).
5)  .
.
33. Дискретні випадкові величини.Функції розподілу і її властивості.
Нехай Ω – простір елементарних подій деякого стохастичного експерименту. Будь-яку функцію  ,
,  , всі значення якої є дійсними числами, називають випадковою величиною.
, всі значення якої є дійсними числами, називають випадковою величиною.
Означення: Величина називається випадковою, якщо внаслідок проведення експерименту під впливом випадкових факторів вона набуває того чи іншого можливого значення з певною ймовірністю.
Можна сказати і так: випадковою величиною х називається функція  , визначена в просторі елементарних подій Ω і така, що для
, визначена в просторі елементарних подій Ω і така, що для 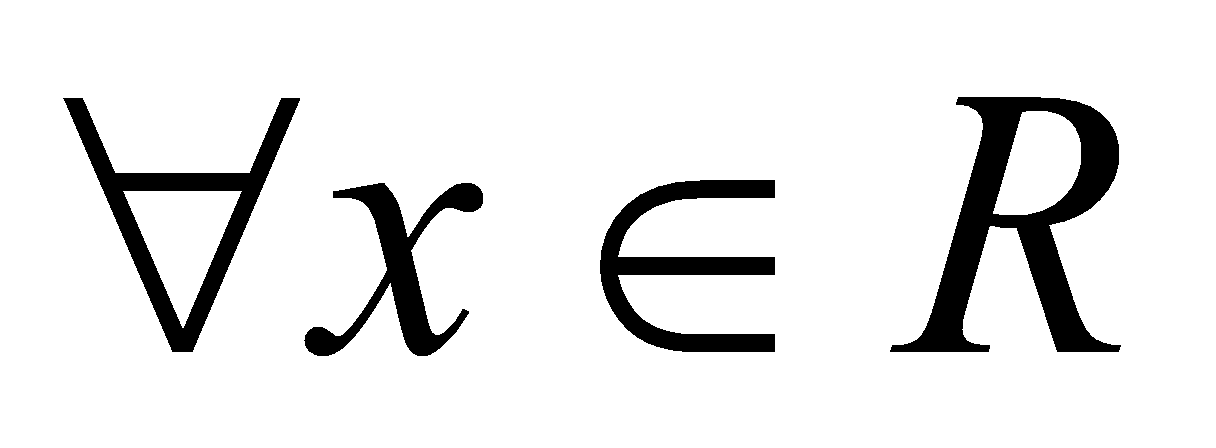 визначена ймовірність події
визначена ймовірність події 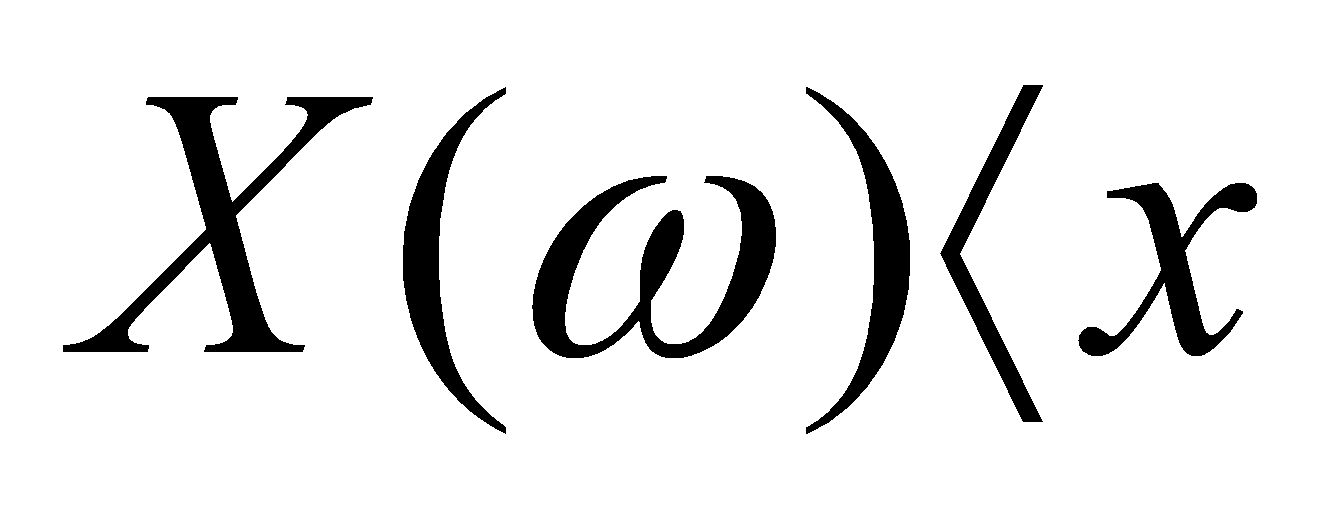 .
.
Означення: Дискретною називається випадкова величина х, яка приймає окремі ізольовані можливі значення з визначеними ймовірностями, тобто величина для якої існує скінченна або злічена множина значень  таких, що
таких, що 
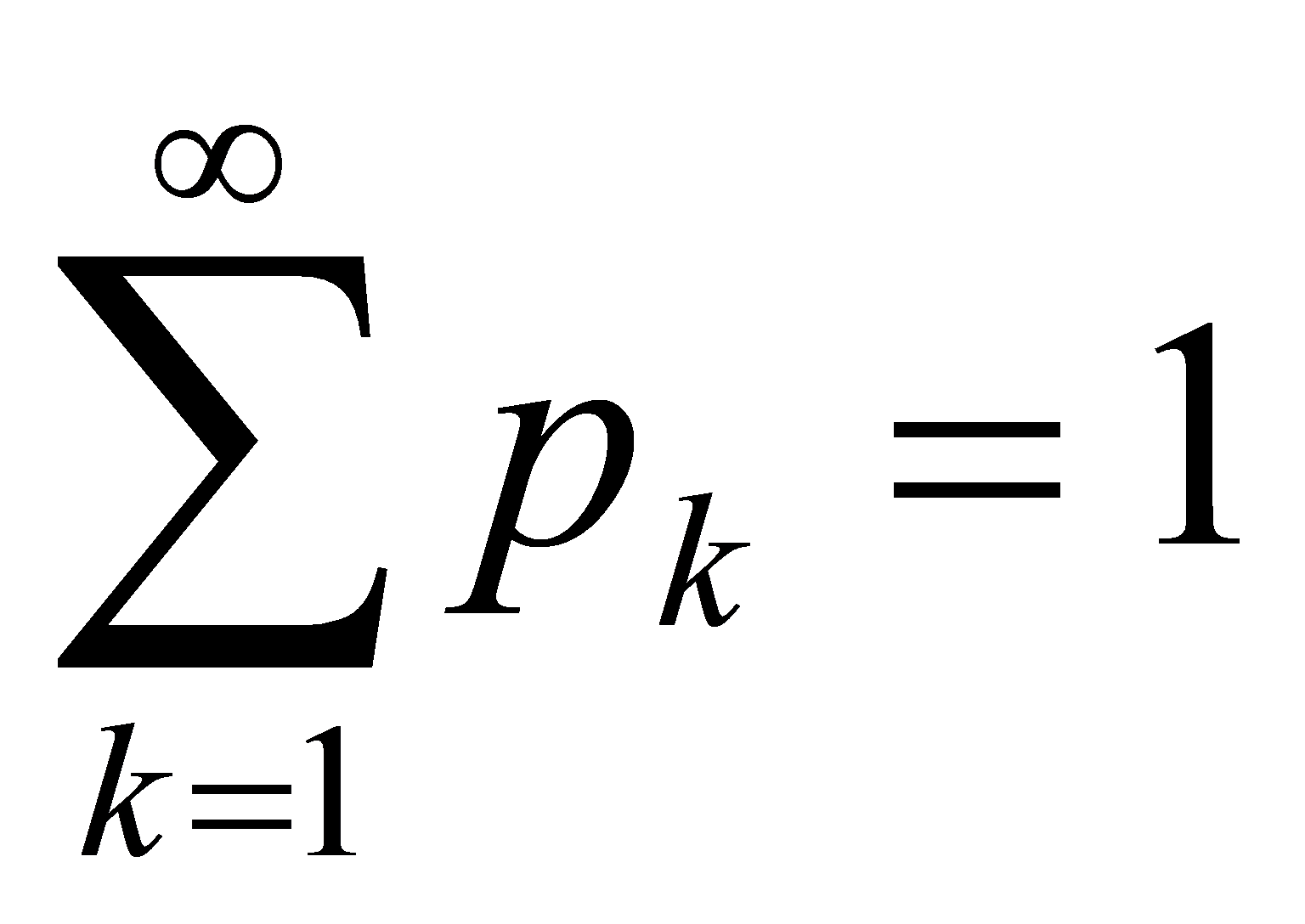 .
.
Інше означення:
Означення: Випадкова величина називається дискретною, якщо її значення можна записати у вигляді послідовності (скінченної або нескінченної).
Випадкову величину позначають великими латинськими літерами, а їх значення малими літерами.
Якщо випадкова величина Х набуває значень  з відповідними ймовірностями
з відповідними ймовірностями 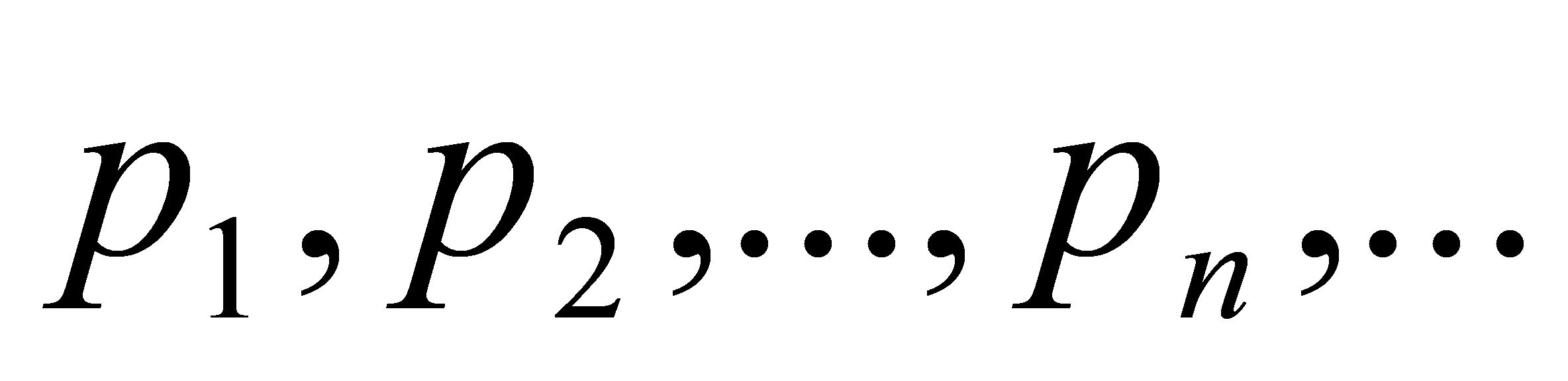 , то говорять, що задано закон розподілу ймовірностей випадкової величини.
, то говорять, що задано закон розподілу ймовірностей випадкової величини.
Закон розподілу випадкової величини зручно записувати у вигляді таблиці:
| Х | х1 | х2 | ... | хn |
| Р | р1 | Р2 | ... | pn |
В даній таблиці 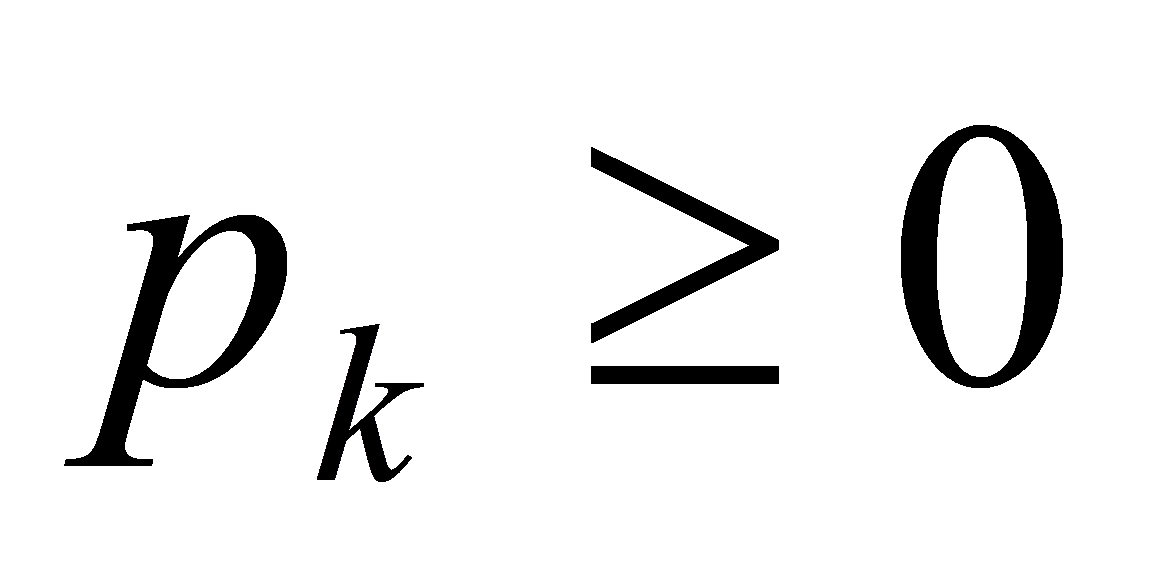 ,
,  . Враховуючи те, що в одному випробування випадкова величина приймає одне і тільки одне можливе значення, робимо висновок, що події
. Враховуючи те, що в одному випробування випадкова величина приймає одне і тільки одне можливе значення, робимо висновок, що події  утворюють повну групу несумісних подій і відповідно сума ймовірностей цих подій рівна одиниці:
утворюють повну групу несумісних подій і відповідно сума ймовірностей цих подій рівна одиниці: 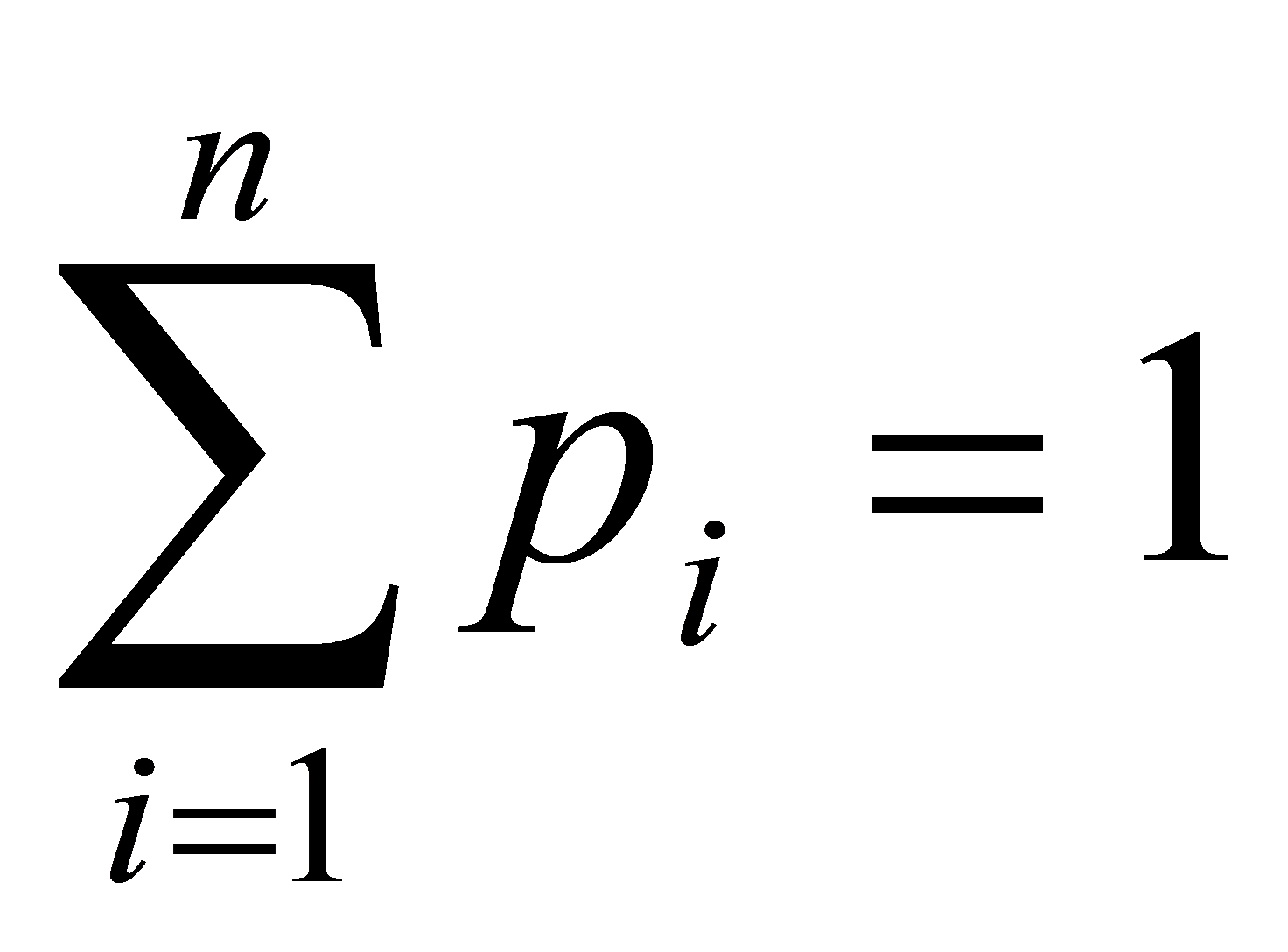 , (1).
, (1).
Формула (1) - це умова нормування для дискретної випадкової величини.
Закон розподілу ймовірностей можна унаочнити графічно. Для цього на осі 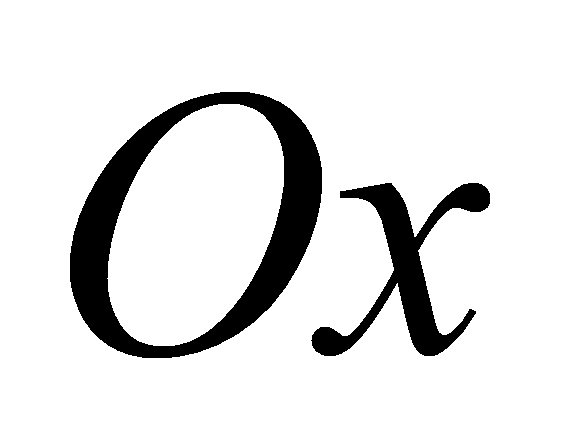 відкладають
відкладають  , на
, на 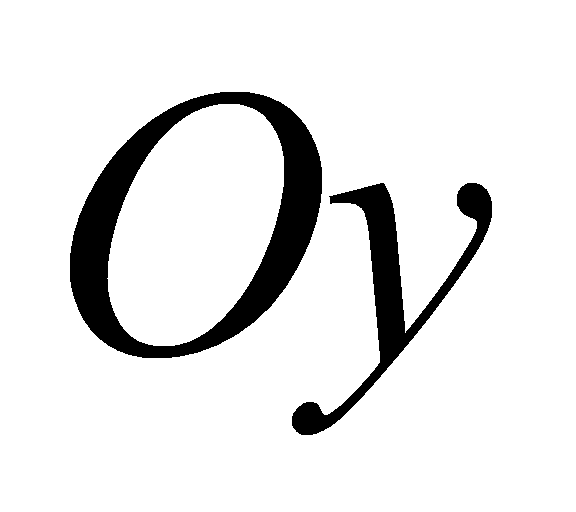 –
–  . Точки з координатами
. Точки з координатами  послідовно сполучають. Утворену фігуру називають імовірнісним многокутником.
послідовно сполучають. Утворену фігуру називають імовірнісним многокутником.
Закон розподілу можна подати як функцію розподілу ймовірностей випадкової величини F(х) або так звану інтегральну функцію.
Означення: Функцію аргументу х, що визначає ймовірність в події Х < х, називається функцією розподілу ймовірностей:  .
.
Властивості функції розподілу:
1) Для 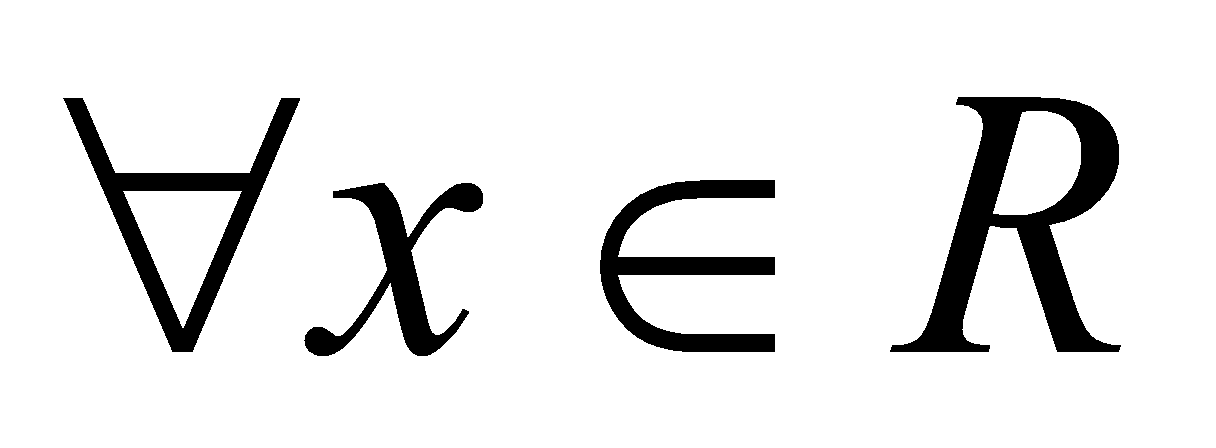 :
: 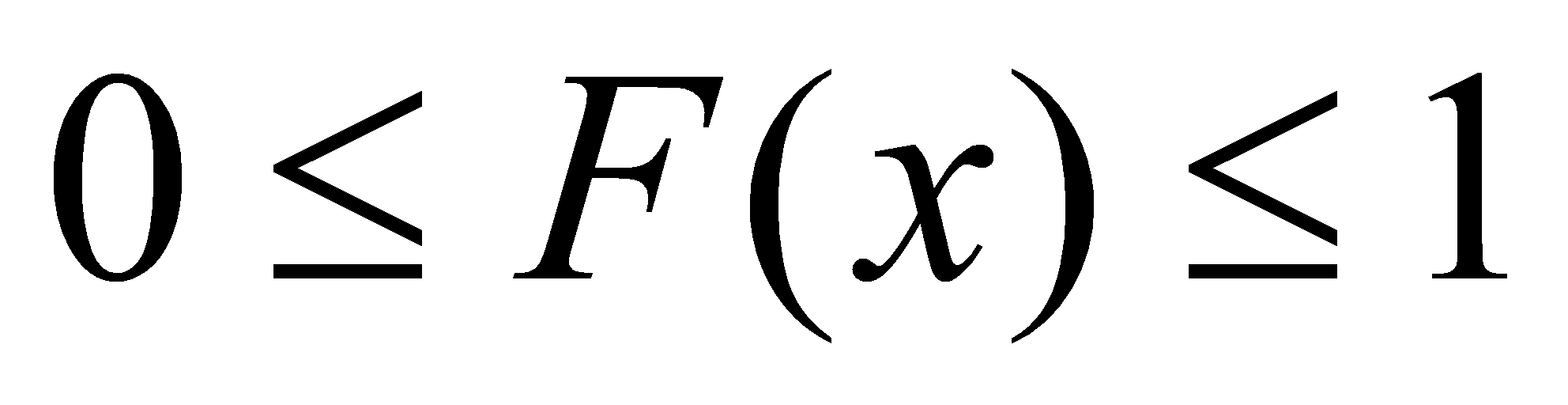 .
.
2) Функція F(x) є не спадною: якщо  , то
, то  .
.
3) Ймовірність того, що випадкова величина Х набуде можливого значення  , дорівнює різниці між значеннями функції розподілу F(х) в правому і лівому кінцях проміжку:
, дорівнює різниці між значеннями функції розподілу F(х) в правому і лівому кінцях проміжку:
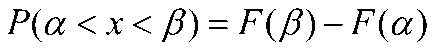
 2020-04-12
2020-04-12 197
197








