Формула Ньютона Лейбніца

Теорема. Якщо функція 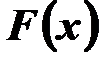є якою-небудь первісною для неперервної функції 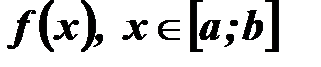, то справедлива формула:

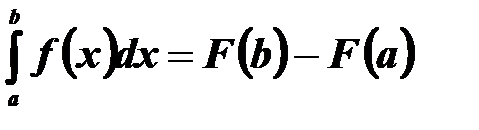   (2)

Формула (2) називається формулою Ньютона-Лейбніца.

Доведення.

Нехай 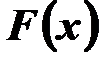- деяка первісна функції 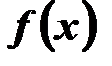. Оскільки інтеграл є також первісною, то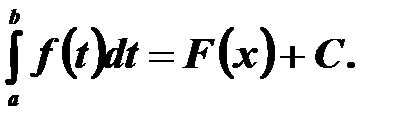

Якщ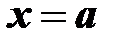о , то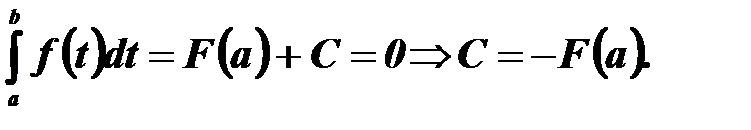

Тоді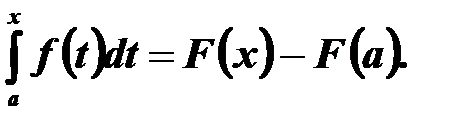

При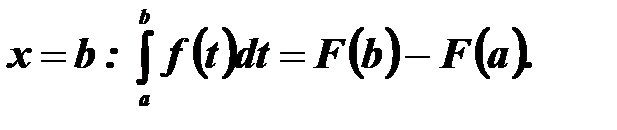

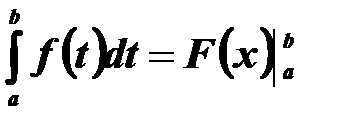
Диференціальні рівняння 1-го порядку з відокремленими змінними.

.

Означення. Диференціальним рівнянням першого порядку називається рівняння виду:

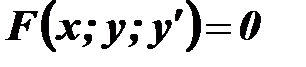                                   (3)

яке зв’язує незалежну змінну х, невідому функцію 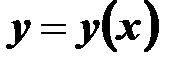та її похідну .

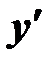Якщо рівняння (3) можна розв’язати відносно 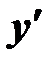, то його записують у вигляді 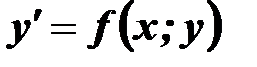і називають рівнянням першого порядку, розв’язаним відносно похідної або рівнянням в нормальній формі.

Теорема Коші (про існування і єдність розв’язку). Нехай функція 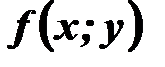і її частинна похідна 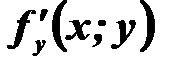визначені і неперервні у відкритій області 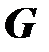площини 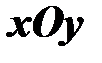і точка 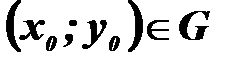. Тоді існує єдиний розв’язок 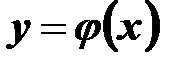, який задовольняє умову 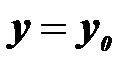при 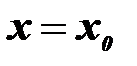, тобто .

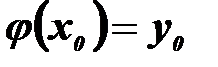Диференціальне рівняння може мати нескінченну кількість розв’язків.

Означення. Функція 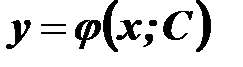, яка залежить від аргументу х і будь-якої сталої С, називається загальним розв’язком рівняння 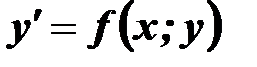в області 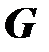, якщо вона задовольняє дві умови:

а) функція 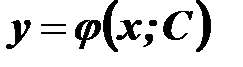є розв’язком рівняння при будь-якому значенні сталої С з деякої множини;

б) для будь-якої точки 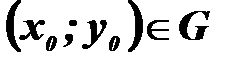можна знайти таке значення С=С₀, що функція 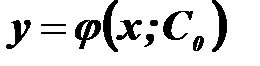задовольняє початкову умову .

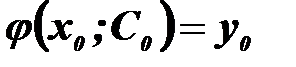Якщо загальний розв’язок диференціального рівняння знайдено в неявному вигляді, тобто у вигляді рівняння 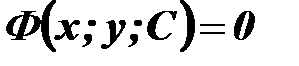, то такий розв’язок називають загальним інтегралом диференціального рівняння.

Означення. Рівняння виду:

,

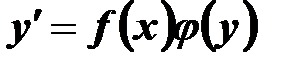де 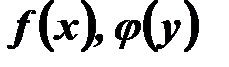задані і неперервні на деякому інтервалі функції, називається диференціальним рівнянням з відокремлюваними змінними.

Якщ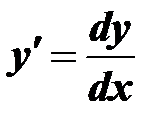о , то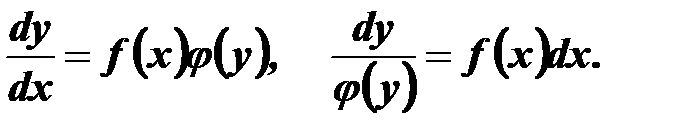

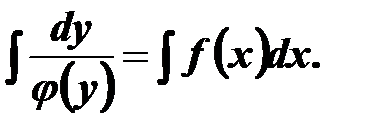
Отже, диференціальне рівняння є розв’язаним у квадратурах.