Возвращение к исходному интегралу

Формула интегрирования по частям применима и для нахождения интегралов вида  и 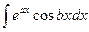, где а и b – числа. При нахождении этих интегралов она применяется последовательно два раза, причем оба раза за u выбирается либо показательная функция, либо тригонометрическая. После двукратного интегрирования по частям получается линейное уравнение относительно искомого интеграла.

Пример 9. Найти I = .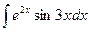

D   Положим 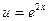, 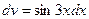. Тогда , .

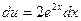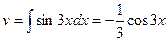Следовательно, I = .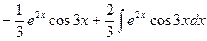

Для вычисления интеграла 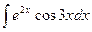снова применим интегрирование по частям. Положим 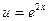, 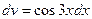. Тогда , .

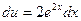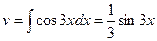Таким образом,                                         

I= = .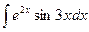

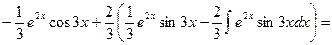
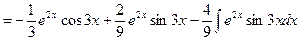Так как в правой части стоит искомый интеграл, то, перенося его в левую часть, получим: 

.

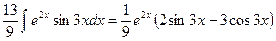Отсюда получаем окончательный результат:

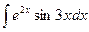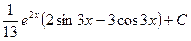= . Ñ

Применим изложенный метод к вычислению еще двух, часто используемых в приложении, интегралов.

Пример 10. Найти I = .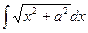

D Положим 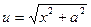, 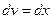. Тогда 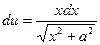, 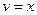. Следовательно,

(*)

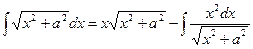
Так как , то

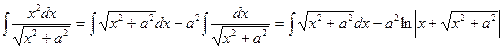
(см. лекция 2, п.2б, пример 20).

Подставив полученное выражение в равенство (*), будем иметь

.

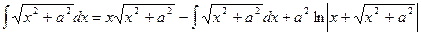Таким образом, 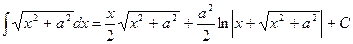. Ñ

Пример 11. Найти 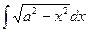,     (а>0)

D Положим , , 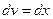откуда , 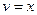. Следовательно,

,

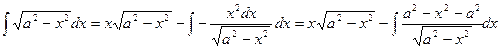или .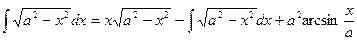

Отсюда получаем: 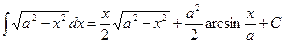. Ñ