Б) Метод подстановки (метод введения новой переменной)

Пусть интеграл 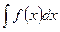 ( 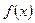 - непрерывна) не может быть непосредственно преобразован к виду табличного. Сделаем подстановку 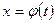, где 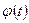 - функция, имеющая непрерывную производную. Тогда 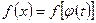,  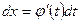 и

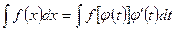.                                                           (3)

Формула (3) называется формулой замены переменной в неопределенном интеграле.

Как правильно выбрать подстановку? Это достигается практикой в интегрировании. Но можно установить ряд общих правил и некоторых приемов для частных случаев интегрирования.

Правило интегрирования способом подстановки состоит в следующем.

1. Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).

2. Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.

3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.

4. Производят замену под интегралом.

5. Находят полученный интеграл.

6. Производят обратную замену, т.е. переходят к старой переменной.

 

Проиллюстрируем правило примерами.

Пример 18. Найти .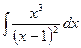

D Положим 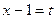, тогда 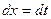,  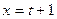  и

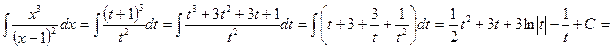
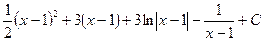= . Ñ

Пример 19. Найти .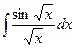

D Вычислим интеграл 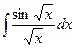 , придерживаясь следующей формы записи:

=  .  

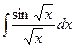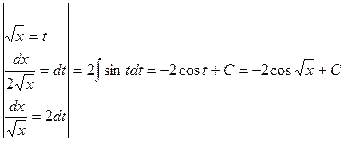Этот интеграл найдем подведением 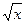под знак дифференциала.

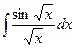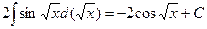= . Ñ

Пример 20. Найти  ().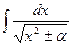

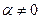D Применим подстановку Эйлера: 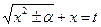, где 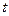- новая переменная.

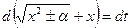, т.е. 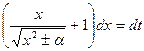, или 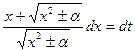. Отсюда 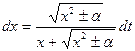, т.е. .

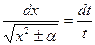Таким образом, имеем 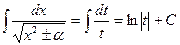. Заменяя  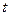его выражением через x, окончательно находим интеграл, играющий важную роль в интегрировании иррациональных функций:  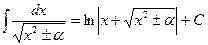  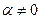  (). Ñ

Студенты прозвали этот интеграл «длинным логарифмом».

Иногда вместо подстановки 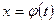 лучше выполнять замену переменной вида .

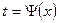Пример 21. Найти  .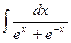

D  Полагая t=e^x , получаем 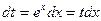,  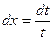и

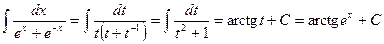. Ñ

Пример 22. Найти  .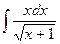

D Воспользуемся подстановкой 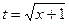. Тогда , , .

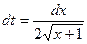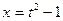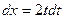Следовательно, 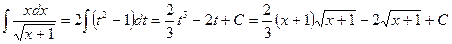. Ñ

В ряде случаев нахождение интеграла основывается на использовании методов непосредственного интегрирования и подведения функций под знак дифференциала одновременно (см. пример 12).

Проиллюстрируем этот комбинированный подход к вычислению интеграла, играющего важную роль при интегрировании тригонометрических функций.

Пример 23. Найти .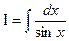

D Имеем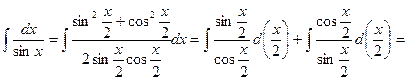

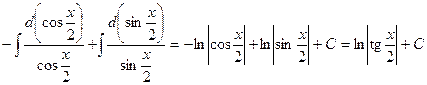= . Ñ

Итак, .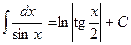

Другой подход к вычислению этого интеграла:

.

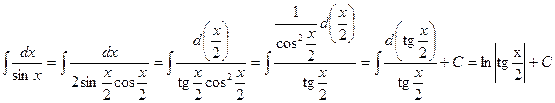Пример 24. Найти  .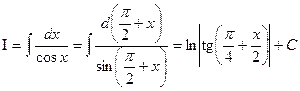

Заметим, что удачный выбор подстановки обычно представляет трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.

Лекция 3.