Непосредственное интегрирование

Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Пример 1. Найти .

D Разделив числитель на знаменатель, получим:

= . Ñ

Отметим, что нет надобности после каждого слагаемого ставить произвольную постоянную, потому что их сумма есть также произвольная постоянная, которую мы пишем в конце.

Пример 2. Найти .

D Преобразуем подынтегральную функцию следующим образом:

Применив табличный интеграл 1, получим:

. Ñ

Пример 3.

Пример 4.

Пример 5.

= .

В некоторых случаях нахождение интегралов упрощается применением искусственных приемов.

Пример 6. Найти .

D Умножив подынтегральное выражение на находим

= . Ñ

Пример 7.

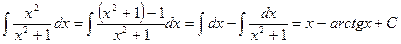Пример 8.

Интегрирование методом замены переменной

Вычислить заданный интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях применяют другие приемы. Одним из наиболее эффективных является метод замены переменной. Сущность его заключается в том, что путем введения новой переменной интегрирования удается свести заданный интеграл к новому, который сравнительно легко берется непосредственно. Существуют два варианта этого метода.

А) Метод подведения функции под знак дифференциала

По определению дифференциала функции .

Переход в этом равенстве слева направо называют "подведением множителя под знак дифференциала".

Теорема об инвариантности формул интегрирования

Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от нее, т.е., если

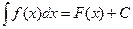, то и ,

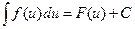где - любая дифференцируемая функция от x. Ее значения должны принадлежать интервалу, в котором функция определена и непрерывна.

Доказательство:

Из того, что , следует . Возьмем теперь функцию . Для ее дифференциала в силу свойства инвариантности формы первого дифференциала функции* имеем

Отсюда .

Пусть требуется вычислить интеграл 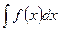. Предположим, что существуют дифференцируемая функция и функция такие, что подынтегральное выражение может быть записано в виде

(1)

Тогда

(2)

т.е. вычисление интеграла сводится к вычислению интеграла и последующей подстановке .

Пример 1. .

Пример 2. .

Пример 3. .

Пример 4. .

Пример 5. .

Пример 6. .

Пример 7. .

Пример 8. .

Пример 9. .

Пример 10. .

Пример 11.

Приведем далее примеры вычисления интегралов, которые нам понадобятся в теории интегрирования рациональных дробей.

Пример 12. Найти I= (a¹0).

D Представим подынтегральную функцию в виде:

Следовательно,

= .

Таким образом, . Ñ

Пример 12а. Найти I= , .

D Так как ,

следовательно I= . Ñ

Пример 13. Найти 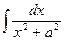(a¹0).

D Для того, чтобы свести этот интеграл к табличному, разделим числитель и знаменатель подынтегрального выражения на :

Мы подвели постоянный множитель под знак дифференциала. Рассматривая как новую переменную, получим:

. Ñ

Вычислим также интеграл, который имеет важное значение при интегрировании иррациональных функций.

Пример 14. Найти I= (½ х ½< а, а ¹0).

D Имеем .

Итак, 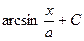(½ х ½< а, а ¹0). Ñ

Представленные примеры иллюстрируют важность умения приводить данное

дифференциальное выражение к виду , где есть некоторая функция от x и g – функция более простая для интегрирования, чем f.

В этих примерах были проведены преобразования дифференциала, такие как

где b – постоянная величина

часто используемые при нахождении интегралов.

В таблице основных интегралов предполагалось, что x есть независимая переменная. Однако, эта таблица, как следует из изложенного выше, полностью сохраняет свое значение, если под x понимать любую непрерывно дифференцируемую функцию от независимой переменной. Обобщим ряд формул таблицы основных интегралов.

3а. .

4. .

5. = .

6. = .

7. = .

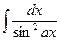8. 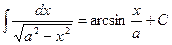(½ х ½< а, а ¹0).

9. (а ¹0).

Операция подведения функции под знак дифференциала эквивалентна замене переменной х на новую переменную . Нижеследующие примеры иллюстрируют это положение.

Пример 15. Найти I= .

D Произведем замену переменной по формуле , тогда , т.е. и I= .

Заменив u его выражением , окончательно получим

I= . Ñ

Выполненное преобразование эквивалентно подведению под знак дифференциала функции .

Пример 16. Найти .

D Положим , тогда , откуда . Следовательно,

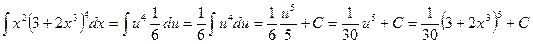. Ñ

Пример 17. Найти .

D Пусть , тогда , или . Следовательно,

. Ñ

В заключение отметим, что разные способы интегрирования одной и той же функции иногда приводят к функциям, различным по своему виду. Это кажущееся противоречие можно устранить, если показать, что разность между полученными функциями есть постоянная величина (см. теорему, доказанную на лекции 1).

Примеры:

а) .