У дискретной случайной величины есть числовые характеристики. Мы рассмотрим три – математическое ожидание, дисперсию и среднеквадратическое отклонение.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
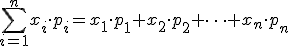
Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
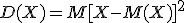
Дисперсию удобно вычислять по формуле:
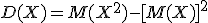
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
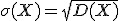
Рассмотрим вычисление числовых характеристик случайной величины на примере.
Найти числовые характеристики случайной величины Х, заданной следующим законом распределения:
| Х | 2 | 3 | 5 |
| р | 0,1 | 0,6 | 0,3 |
Решение
Найдём математическое ожидание:
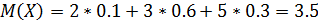
Напишем закон распределения для случайной величины 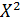
| Х | 4 | 9 | 25 |
| р | 0,1 | 0,6 | 0,3 |
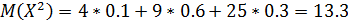
Вычислим дисперсию:
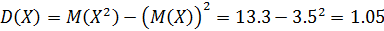
Среднеквадратичное отклонение:
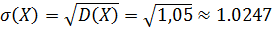
 2020-04-12
2020-04-12 168
168







