2020-04-07
127
1°. Элементы сходящейся последовательности имеют вид: 
, где 
, 
– бесконечно малая последовательность, 
.
2°. Сходящаяся последовательность имеет только один предел.
3°. Сходящаяся последовательность ограничена.
Обратное утверждение неверно, например, последовательность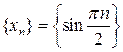 
является ограниченной, но предела не имеет.
4°. Сумма, разность, произведение и также частное (при условии, что 
и 
), двух сходящихся последовательностей 
и 
есть сходящаяся последовательность, и ее предел равен соответственно сумме, разности, произведению и частному пределов исходных последовательностей.
Следствие. Арифметические операции над сходящимися последовательностями приводят к таким же операциям над их пределами.
5°. Если элементы сходящейся последовательности , начиная с некоторого номера, удовлетворяют неравенству 
(
), то и предел этой последовательности 
удовлетворяет неравенству 
(
).
Следствия.
1) Если элементы 
и 
сходящихся последовательностей и , начиная с некоторого номера, удовлетворяют неравенству 
, то их пределы удовлетворяют такому же неравенству: 
.
2) Если все элементы сходящейся последовательности находятся на отрезке 
, то и ее предел также находится на этом отрезке.
6°. Пусть и 
– сходящиеся последовательности и 
. Пусть, начиная с некоторого номера, элементы последовательности 
удовлетворяют неравенствам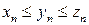 
. Тогда последовательность 
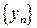сходится, и 
.
7°. Последовательность 
, извлеченная из элементов данной последовательности 
с сохранением порядка, называется ее подпоследовательностью.
Любая подпоследовательность сходящейся последовательности сходится к тому же пределу.
