Свойства бесконечно малых последовательностей

1°. Бесконечно малая последовательность ограничена.

2°. Сумма и разность двух бесконечно малых последовательностей дает бесконечно малую последовательность.

3°. Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.

4°. Произведение двух бесконечно малых последовательностей есть последовательность бесконечно малая.

5°. Если элементы бесконечно малой последовательности  не равны нулю, то последовательность  будет бесконечно большой.

6°. Если  бесконечно большая последовательность и 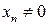, то последовательность  – бесконечно малая.

Примерыбесконечно малых последовательностей:

1) Бесконечно убывающая геометрическая прогрессия x_n = qⁿ при |q| <1 является бесконечно малой последовательностью, т.к. для любого e > 0 из неравенства  следует, что при  неравенство выполняется, начиная с номера .

2) Последовательность  – бесконечно малая, т.к. ее элементы являются произведением элементов ограниченной последовательности  и бесконечно малой последовательности .

3) Последовательность  – бесконечно малая, т.к. является суммой бесконечно малых последовательносте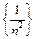й  и .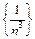

4) Последовательность  – бесконечно малая, т.к. является произведением бесконечно малой последовательности 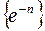 на бесконечно малую последовательность .

Замечание. Последовательности { n^a } при a >0 являются бесконечно большими, а при a <0 - бесконечно малыми последовательностями.