Построение доверительных интервалов для математического ожидания и дисперсии, соответствующих доверительной вероятности

 

Чтобы иметь представление о точности и надежности оценок (1.16 – 1. 18) в математической статистике используется понятие доверительного интервала. Пусть для некоторого параметра a (математического ожидания или дисперсии) получена несмещенная оценка μ. Назначим некоторую достаточно большую вероятность γ (доверительную вероятность) и найдем такое значение ε, при котором вероятность равна (1.19):

 

 (1.19)

 

Равенство (1.19) означает, что с вероятностью γ интервал Iγ, который называется доверительным интервалом, накрывает неизвестное значение параметра a.

 

 (1.20)

 

При построении доверительного интервала для математического ожидания используют то обстоятельство, что оценка (1.16) представляет собой сумму n независимых одинаково распределенных случайных величин X_i и, согласно центральной предельной теореме, при достаточно больших n ее закон распределения близок к нормальному закону. В этом случае доверительный интервал для оценки математического ожидания можно представить в виде

 

 (1.21)

 

где tγ – квантиль нормального распределения, который определяется по статистическим таблицам.

Границы доверительного интервала вычислены по формулам (1.22-1.23).

 

, (1.22)

, (1.23)

 

Определенный доверительный интервал (1.21) является приближенным, так как вместо точного значения дисперсии используется ее оценка Dn. Величина tγ определяет для нормального закона число стандартных отклонений, которое нужно отложить вправо и влево от оценки математического ожидания для того, чтобы вероятность попадания в полученный интервал была равна γ.

Существуют более точные методы определения доверительного интервала. Например, методы определения доверительного интервала для оценки математического ожидания на основе распределения Стьюдента, где вместо квантиля нормального распределения используется квантиль распределения Стьюдента, который также находится по таблицам.

 

, (1.24)

,

, (1.25)

 

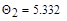
Теоретическое значение математического ожидания входит в доверительный интервал. Аналогично может быть получен доверительный интервал для дисперсии. Оценка дисперсии также представляет собой сумму n случайных величин. Однако эти величины уже нельзя считать независимыми, так как в любую из них входит оценка Xmean. Но и этом случае при увеличении n закон распределения их суммы также приближается к нормальному. Поэтому доверительный интервал для дисперсии определяется так же, как и для математического ожидания и имеет вид:

 

I_γ=(Dn-ε, Dn+ε),

 

где ε вычисляется по формуле (1.26):

 

, (1.26)

 

где Dd – дисперсия оценки Dn.

 

, (1.27)

 

Конечные формулы границ доверительного интервала имеют вид:

 

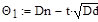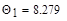,  (1.28)

,  (1.29)

 

Более точный доверительный интервал для оценки дисперсии может быть получен при нормальном распределении на основе распределения χ². Однако в отличие от нормального распределения и распределения Стьюдента распределение χ² не является симметричным распределением. Поэтому выберем интервал I_γ так, чтобы вероятность выхода величины вправо и влево были одинаковы и равны 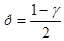 и . Чтобы построить интервал с таким свойством, необходимо воспользоваться таблицами распределения χ². В этом случае доверительный интервал для оценки дисперсии в соответствии с обозначением примет вид:

 

,

 

где Dn – несмещённая оценка,

χ1², χ2² - могут быть найдены по стандартной программе Mathcad (1.30-1.31).

 

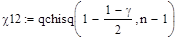, (1.30)

, (1.31)

 

Конечные формулы границ доверительного интервала имеют вид:

 

, ,

,

 

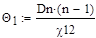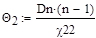Несмещённая оценка входит в доверительный интервал (D=σ², σ² - стандартное отклонение).