Предел функции двух переменных

 – предел функции двух переменных в точке.

Основные теоремы о пределах

1. 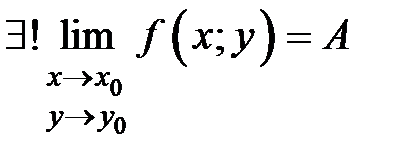  – если предел функции двух переменных существует, то он единственный.

2.

.

3. .

4. .

5. .

6. .

7. , .

Непрерывность функции в точке

Условия непрерывности функции в точке

1.  определена в точке  и в некоторой окрестности этой точки.

2. 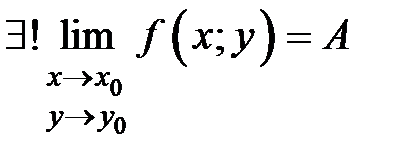.              3. .

Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Точки разрыва функции 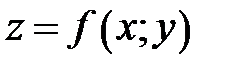 могут образовывать целые лини разрыва.

Частные производные первого порядка

  – частная производная функции  в точке  по переменной х.

  – частная производная функции  в точке  по переменной у.

  – угловой коэффициент касательной к сечению поверхности  плоскостью .

  – угловой коэффициент касательной к сечению поверхности  плоскостью .

Частные производные высших порядков

Частные производные второго порядка функции ,  смешанные частные производные второго порядка:

.

Частные производные третьего порядка функции ,  смешанные частные производные третьего порядка.

.

Теорема Шварца. Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.

Дифференцируемость и полный дифференциал

Если функция  дифференцируема в точке , то она непрерывна в этой точке, имеет в ней частные производные  и 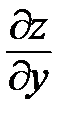  –необходимое условие дифференцируемости функции.

Если функция 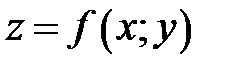 имеет непрерывные частные производные  и 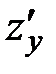 в точке , то она дифференцируема в этой точке и ее полный дифференциал выражается формулой:   –достаточное условие дифференцируемости функции.

  –полный дифференциал первого порядка функции двух переменных.

  –частный дифференциал первого порядка функции двух переменных.

  –частный дифференциал первого порядка функции двух переменных.