 – дифференциал второго порядка функции двух переменных.
– дифференциал второго порядка функции двух переменных.
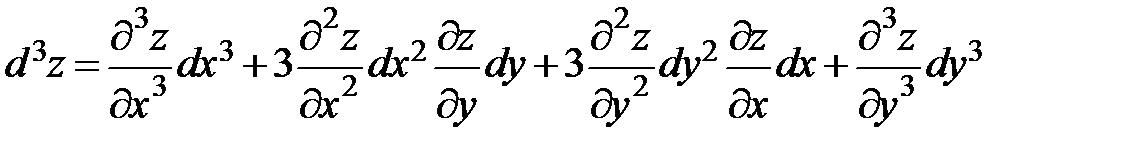 – дифференциал третьего порядка функции двух переменных.
– дифференциал третьего порядка функции двух переменных.
Производной сложной функции
 – сложная функция одной независимой переменной t.
– сложная функция одной независимой переменной t.
 – производная сложной функции одной независимой переменной t.
– производная сложной функции одной независимой переменной t.
Производной неявной функции
 – неявная функция двух переменных.
– неявная функция двух переменных.
 – производная неявной функции по переменной х.
– производная неявной функции по переменной х.
 – производная неявной функции по переменной у.
– производная неявной функции по переменной у.
Касательная плоскость и нормаль к поверхности
 – уравнение касательной плоскости к графику функции
– уравнение касательной плоскости к графику функции 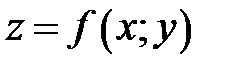 в точке
в точке  .
.
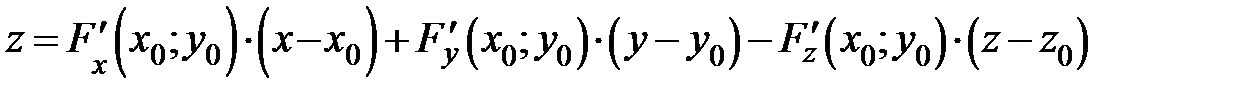 – уравнение касательной плоскости к графику функции
– уравнение касательной плоскости к графику функции  в точке
в точке  .
.
 – уравнение нормали к поверхности
– уравнение нормали к поверхности 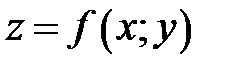 в точке
в точке  .
.
 – ура уравнение нормали к поверхности
– ура уравнение нормали к поверхности  в точке
в точке  .
.
Экстремум функции двух переменных
 –
–  точка минимума функции.
точка минимума функции.
 –
–  точка максимума функции.
точка максимума функции.
Точки минимума и максимума называются точками экстремума, а значения функции в этих точках называются экстремумами функции.
Точки, в которых производная функции обращается в ноль или не существует, называются критическими точками.
Если функция  имеет экстремум в точке
имеет экстремум в точке  , то
, то  ,
,  – необходимое условие существования экстремума.
– необходимое условие существования экстремума.
Достаточное условие существования экстремума
Пусть функция  имеет непрерывные частные производные в точке
имеет непрерывные частные производные в точке  до второго порядка включительно
до второго порядка включительно  ,
,  ,
,  и
и  .
.
Если  , то функция
, то функция  в точке
в точке  имеет экстремум: максимум, если
имеет экстремум: максимум, если  ; минимум, если
; минимум, если 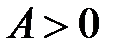 .
.
Если  , то функция
, то функция  в точке
в точке  экстремума не имеет.
экстремума не имеет.
Если  экстремум в точке
экстремум в точке  может быть, может не быть, необходимы дополнительные исследования.
может быть, может не быть, необходимы дополнительные исследования.
 2020-04-12
2020-04-12 186
186








