Понятие случайной величины. Закон распределения дискретной случайной величины

Глава 3. Случайные величины.

 

Случайной величиной называется переменная величина, которая в результате испытания может принять одно из возможных своих значений, причем неизвестно заранее, какое именно.

Существуют дискретные и непрерывные случайные величины.

Случайная величина называется дискретной, если множество ее возможных значений – отдельные изолированные числа, причем это множество конечное или бесконечное, но обязательно счетное.

Например, количество дождливых дней в июне или число произведенных выстрелов до первого попадания.

Случайная величина называется непрерывной, если ее возможные значения непрерывно заполняют некоторый промежуток (конечный или бесконечный) числовой оси.

Например, ошибка взвешивания или дальность полета снаряда.

Случайные величины обычно обозначают прописными буквами латинского алфавита X, Y, Z,…, а их значения строчными буквами x, y, z,….

Случайная величина описывается законом распределения.

Закон распределения случайной величины устанавливает связь между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения дискретной случайной величины X может быть задан в виде таблицы (см. рис. 3.1.1), первая строка которой содержит в порядке возрастания возможные значения x_i, а вторая – вероятности p_i этих значений.

Такая таблица (рис. 3.1.1) называется рядом распределения.

 

x1	x2	…	xn
p1	p2	…	pn

        X:

 

 

                      Рис. 3.1.1

 

Отметим, что .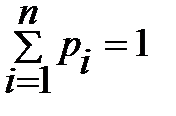

Если множество возможных значений X бесконечно, то .

Закон распределения дискретной случайной величины может быть также задан аналитически

                            P(X = x_i) = φ(x_i)                                            (3.1.1)                                         

или с помощью функции распределения (раздел 3.2).

Кроме того, закон распределения дискретной случайной величины можно изобразить графически, а именно в прямоугольной системе координат строят точки M₁(x₁,p₁), M₂(x₂,p₂), …, M_n(x_n,p_n) и соединяют их отрезками прямой. Полученную фигуру называют многоугольником распределения.

Введем понятие независимых случайных величин.

Две случайные величины называют независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина.

Определим математические операции над дискретными случайными величинами.

Пусть даны две случайные величины:

x1	x2	…	xn
p1	p2	…	pn

 

X:

 

y1	y2	…	ym
p1	p2	…	pm

 

Y:

 

            Рис. 3.1.2

Тогда случайная величина kX, где k – const, принимает значения kx_i с теми же вероятностями p_i, , а случайная величина X^m принимает значения с вероятностями , .

 

3.1.1. Дана случайная величина

 

-2	-1	0	1	2
0,2	0,1	0,3	0,3	0,1

X:

 

Найти закон распределения случайных величин: 1) Y = -2 X; 2) Z = X ².

Решение.

1) Значения Y будут: -2 (-2) = 4; (-2) (-1) = 2; (-2) 0 = 0; (-2) 1 = -2; (-2) 2 = -4 с теми же вероятностями 0,2; 0,1; 0,3; 0,3; 0,1, но записывать их надо в порядке возрастания, т.е.

 

-4	-2	0	2	4
0,1	0,3	0,3	0,1	0,2

Y:

 

2) Значения Z будут: (-2)² = 4; (-1)² = 1; 0² = 0; 1² = 1; 2² = 4.

Одинаковые значения учитываются только один раз, при этом их вероятности складываются. Так, P (Z = 4) = 0,2 + 0,1 = 0,3. Следовательно,

 

0	1	4
0,3	0,4	0,3

Z:

 

Суммой (разностью или произведением) случайных величин X и Y называется случайная величина, принимающая все возможные значения вида x_i + y_j (x_i­ – y_j или x_iy_j) с вероятностями P_ij, где P_ij = P [(X = x_i, Y = y_j­)] – вероятность того, что X примет значение x_i, а Y – значение y_j, , .

3.1.2. Даны законы распределения двух независимых случайных величин

-1	0	1
0,2	0,3	0,5

 

1	2	3
0,3	0,5	0,2

X:                                                  Y:       

                                       

Найти закон распределения случайной величины Z = X + Y.

Решение. Составим вспомогательную таблицу, в каждой внутренней клетке которой в левом углу запишем значения суммы X + Y, а в правом углу – вероятности этих значений (см. рис. 3.1.3).

 

	yj	-1	0	1
xi	pj pi	0,2	0,3	0,5
1	0,3	0                 0,06	1      0,09	2      0,15
2	0,5	1      0,01	2      0,15	3      0,25
3	0,2	2      0,04	3      0,06	4        0,1

Рис. 3.1.3

Так как среди значений Z имеются одинаковые, то соответствующие вероятности необходимо сложить. Например, Z = X + Y = 1 получено, если X = 2,      

Y = -1 с вероятностью 0,1 и X = 1, Y = 0 с вероятностью 0,09. Поэтому P (Z =1) = =0,1 + 0,09 = 0,19. В результате получим распределение Z:

 

0	1	2	3	4
0,06	0,19	0,34	0,31	0,1