Числовые характеристики непрерывной случайной величины

Математическое ожидание непрерывной случайной величины X определяется равенством

                                      M(X) =                                                    (3.5.1)

В частности, если все возможные значения X принадлежат интервалу (a,b), то

                                                                                         (3.5.2)

Дисперсия непрерывной случайной величины X определяется равенством

                            D(X) =                                            (3.5.3)

Все свойства M(X) и D(X), рассмотренные в разделе 3.2 для дискретной случайной величины, справедливы и для непрерывных случайных величин.

Для описания случайной величины применяется целый ряд числовых характеристик (помимо M(X) и D(X)).

Модой M₀(X) случайной величины X называется ее наиболее вероятное значение (для которого вероятность P_i или плотность вероятности φ(x) достигает максимума).

Медианой M_e(X) непрерывной случайной величины X называется такое ее значение, для которого

P(X < M_e(X)) = P(X > M_e(X)) = .

Геометрически медиану можно истолковать как точку, в которой ордината графика φ(x) делит пополам площадь, ограниченную кривой распределения (см. рис. 3.5.1)

            

           φ(x)

 

   

 

                            

                0      M_e(X)                                     x

 

 

                            Рис. 3.5.1

Начальным моментом k -ого порядка случайной величины X называется математическое ожидание k -ой степени этой величины:

.

Если X – дискретная случайная величина, то

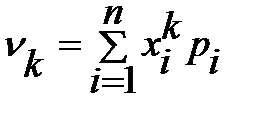                                                                                                  (3.5.4)

Если X – непрерывная случайная величина, то

                                                                                          (3.5.5)

Центральным моментом k -ого порядка случайной величины X называется величина

и

Для дискретной величины

                                                                                       (3.5.6)

Для непрерывной величины

                                                                                (3.5.7)

Напомним, что для обозначения математического ожидания используется буква “ a ”.

 

3.5.1. Дана функция распределения случайной величины X:

1) Найти плотность распределения;

2) вычислить M(X), D(X), M₀(X) и M_e(X).

Решение:

1) φ(x) = F (x) =

2) По формуле (3.5.2): a = M(X) =  = = .

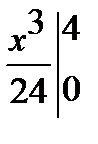Используя формулу (3.2.3), получим

  D(X) = M(X²) – a ² = .

Плотность φ(x) принимает максимальное значение при x = 4. Следовательно, M₀(X) = 4.

Медиану M_e(X) = m найдем из условия F(m) =  или .

 

3.5.2. Случайная величина X задана дифференциальным законом распределения

Найти M(X) и D(X).

Решение.

M(X) =

.

Заметим, что если φ(x) симметрична относительно прямой x = a, то математическое ожидание для такого распределения равно a. В нашем случае φ(x) симметрична относительно прямой x = , а значит M(X) = .

Дисперсию вычислим по формуле

Дважды интегрируя по частям найдем

и .

 

3.5.3. Случайная величина X задана плотностью распределения

Найти: M(X), M₀(X), M_e(X).

 

Решение. Представим функцию φ(x) в виде:

φ(x) = .

Это распределения симметрично относительно x = 3. Следовательно, M(X) = 3. Очевидно, что при x = 3 плотность распределения достигает максимума; следовательно, M₀(X) = 3. В силу симметрии распределения

P(X < 3) = P(X > 3) =    и M_e(X) = 3.