Функция распределения случайной величины

Для описания закона распределения случайной величины X можно рассматривать не вероятность события X=x, а вероятность события X < x, где x – переменная.

Тогда вероятность P(X < x) является некоторой функцией x. Подобное описание случайной величины X применимо как для дискретных, так и для непрерывных случайных величин.

Функцией распределения случайной величины X называется функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x:

                                             F(X) = P(X < x)                                                  (3.3.1).

Функцию F(x) иногда называют интегральной функцией распределения.

 

3.3.1. Дан ряд распределения случайной величины X:

 

2	4	6	7	9
0,2	0,1	0,3	0,3	0,1

 

Найти и изобразить графически функцию F(x).

Решение. Если x 2, то F(x) = 0. Действительно, так как величина X не принимает значений, меньших числа 2, то P(X < x) = 0.

Если 2< x ≤4, то X может принять только значение 2 с вероятностью 0,2. Следовательно, F(x) = 0,2.

Если 4< x ≤6, то X может принять либо значение 2 с вероятностью 0,2, либо значение 4 с вероятностью 0,1. Тогда одно из этих значений, неважно какое, X может принять с вероятностью 0,2 + 0,1 = 0,3 и F(x) = 0,3.

Если 6< x ≤7, то F(x) = 0,2 + 0,1 + 0,3 = 0,6. Действительно, X может принять любое их трех значений: 2, 4, 6.

Если 7< x ≤9, то F(x) = 0,2 + 0,1 + 0,3 + 0,3 = 0,9.

Если x >9, то F(x) = 1. Действительно, событие X ≤ 9 достоверно и вероятность его равна единице.

Итак, искомая функция распределения имеет вид:

 

График F(x) приведен на рис. 3.3.1.

 

                        F(x)

 

                             1  

                          0,9

 

                          0,6

 

                          0,3

                             0,2

                                        

                                       2      4      6  7       9                                 x                                         

Рис. 3.3.1

 

 

Этот пример позволяет сделать вывод о том, что функция распределения любой дискретной величины является разрывной ступенчатой функцией, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений.

Заметим, что для непрерывной случайной величины X функция распределения F(x) является непрерывной.

 

Функция распределения обладает следующими свойствами.

1. Значения F(x) принадлежат отрезку [0;1]: 0 ≤ F(x) ≤ 1.

2. Функция F(x) является неубывающей функцией: F(x₂) ≥ F(x₁), если x₂ > x₁.

3. Вероятность попадания случайной величины X в интервал [ x₁,x₂) равна приращению F(x) на этом интервале: P (x₁ ≤ X < x₂) = F(x₂) – F(x₁).

4. Если все возможные значения случайной величины X принадлежат интервалу (a,b), то F(x) = 0 при x ≤ a и F(x) = 1 при x ≥ b.

 

5. Справедливы следующие предельные соотношения:

lim F(x) = 0, lim F(x) = 1.

3.3.2. Случайная величина X задана функцией распределения

               

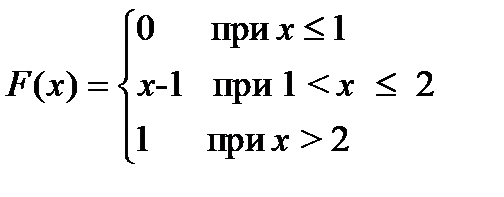
Найти вероятность того, что случайная величина примет значения в интервале [1; 1,5).

Решение. По свойству 3 для F(x) имеем P (1 ≤ X < 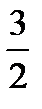) = F () – F (1) = 0,5 – 0 =

= 0,5.

3.3.3. Случайная величина X задана функцией распределения

Найти вероятность того, что случайная величина X примет значения: 1) меньше 2; 2) не меньше 2,5.                                                

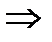Решение. Так как F(x) – непрерывная функция, то должно выполняться F (1) = 0 и F (3) = 1. Тогда, a (3-1)² = 1 a = .

1) Вычислим P (X < 2) = P (1 ≤ X < 2) = F (2) – F (1) = . Действительно, событие (X < 2) равносильно событию (1 ≤ X < 2), так как все возможные значения X сосредоточены на интервале [1,3].

2) Вычислим P (X ≥ 2,5) = P (2,5 ≤ X < 3) = F (3) – F (2,5) = 1 - = 0,4375.