Частица в потенциальной яме

 с бесконечно высокими стенками

Физический смысл волновой функции остается таким же, как и у волны де Бройля:

квадрат модуля волновой функции определяет вероятность обнаружения микрочастицы   в данном месте пространства

в момент времени t.

   

                                     .    (4.1)

Возьмем элемент объема dV (иначеего обозначают как d ³ r, в декартовой системе координат (x, y, z) →

dV = dx ۰ dy ۰ dz, в сферической системе координат

(r, θ, φ) → dV = r ² ۰ dr ۰ dΩ, где dΩ = sinθ ۰ dθ ۰ dφ

– элемент телесного угла). Тогда дифференциальная вероятность dw обнаружить микрочастицу в этом элементе объема будет (по М. Борну):

          .             (4.2)

Величина 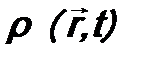   называется плотностью вероятности:

               .               (4.3)

По теореме сложения вероятностей вероятность обнаружить микрочастицу вообще где-то в пространстве  будет достоверным событием. Следовательно,

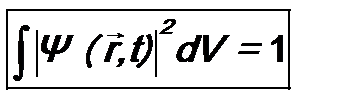                      .                     (4.4)

Это условие нормировки волновой функции. Оно используется для определения произвольной константы, которая обычно возникает при нахождении волновой функции. Эта константу называют нормировочной.

От волновой функции требуется выполнение стандартных условий. Это:

А) конечность; б) непрерывность; в) однозначность.

Суммируем сказанное.

Если микрочастица не одна и их количество N, то волновая функция будет зависеть от координат всех микрочастиц: . Тогда величина дает в момент времени t вероятность одновременного обнаружения

всех частиц, каждую в своей пространственной точке  (i = 1, 2,…, N).

Условие нормировки будет иметь вид:

        .

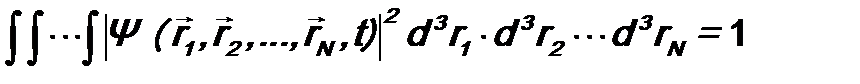Часто весь набор координат    обозначают одной буквой ξ, т.е. ξ = ( ). Тогда  .

Лекция 5

МАТЕМАТИЧЕСКИЙ ФОРМАЛИЗМ КВАНТОВОЙ МЕХАНИКИ. ОПЕРАТОРНЫЙ ФОРМАЛИЗМ

 

Микрочастицы обладают как свойствами частиц, так и волн – это «корпускулярно-волновой дуализм». Как следствие, математический аппарат классической физики для них не применим. Для описания состояния микрочастиц используется операторный формализм.

    

Пусть имеются две функции одного класса:  и . Если есть математическая операция (обозначим ее ), которая переводит функцию  в функцию , т.е. = , то  - это и есть оператор.

Иными словами, оператор – это символ, который показывает, какое действие следует произвести над функцией данного класса, чтобы получить другую функцию того же класса.