Для того, чтобы вычислить определитель матрицы произвольного размера необходимо разложить его по строке или столбцу

Рассмотрим правила, связанные с разложением.

Правило1: Определитель матрицы равен сумме произведений элементов строки определителя на их алгебраические дополнения:

 

 

	n
det(A) =	Σ	aij·Aij - разложение по i-той строке
	j = 1

Правило: Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:

	n
det(A) =	Σ	aij·Aij - разложение по j-тому столбцу
	i = 1

При разложении определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.

Пример 3.

Найти определитель матрицы A

A =	2 4 1 0 2 1 2 1 1

Решение: Вычислим определитель матрицы разложив его по первому столбцу:

det(A) =

2 4 1 0 2 1 2 1 1

=

 

= 2·(-1)1+1·

2 1 1 1

+ 0·(-1)2+1·

4 1 1 1

+ 2·(-1)3+1·

4 1 2 1

=

= 2·(2·1 - 1·1) + 2·(4·1 - 2·1) = 2·(2 - 1) + 2·(4 - 2) = 2·1 + 2·2 = 2 + 4 = 6.

Пример 4.

Дана система четырех линейных алгебраических уравнений. Решить систему методом Крамера.

Решение.

Найдем определитель матрицы коэффициентов при неизвестных. Для этого разложим его по первой строке.

Найдем составляющие определителя:

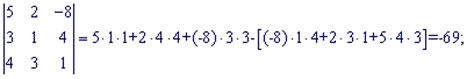
Подставим найденные значения в определитель

Детерминант , следовательно,  система уравнений совместная и имеет единственное решение. Вычислим определители по формулам Крамера:

Разложим каждый из определителей по столбцу в котором есть больше нулей.

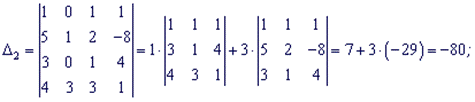
По формулам Крамера находим

Решение системы: х₁=7, х₂=-8, х₃=-5, х₄=6.

 

 

              

 

ПРАКТИЧЕСКАЯ ЧАСТЬ