Линейные операции над векторами

К линейным операциям относятся операции сложения и вычитания

векторов, умножение вектора на число. Рассматривать будем лишь свободные векторы.

Напомним два правила сложения векторов. Пусть даны три вектора

a, b, c (рис. 6).

Рис. 6.

a) Правило треугольника. От произвольно выбранной точки откладываем

вектор, равный вектору а; от его конца откладываем вектор, равный вектору b; строим вектор, начало которого совпадает с началом первого вектора, а конец –с концом второго вектора, это и есть вектор а + b (рис. 6а). Аналогично получается сумма любого конечного числа векторов (рис. 6б).

Рис. 6а. Рис. 6б.

б) Правило параллелограмма. От произвольно выбранной точки откладываем

оба вектора-слагаемые а и b; на этих двух векторах, как на сторонах, строим

параллелограмм. Направленная диагональ этого параллелограмма, выходящая из общего начала векторов а и b представляет вектор а + b (рис. 7).

Рис.7

Определение. Разностью векторов а и b называется вектор m = a - b

такой, что b = m - a (рис 8). На рис. 7 вектор m = a - b есть другая диагональ

параллелограмма с направлением от конца вектора b к концу вектора а.

Заметим, что вектор - b является противоположным вектору b.

Рис.8

Определение. Произведением вектора а на число λ называется вектор λ а, 1) коллинеарныйвектору а,

2) имеющий длину |l | ∙ | a |,

3) направленный так же, как вектор а, если λ > 0, и противоположно, если λ < 0 (рис. 9).

Рисунок 9

Определение. Орт вектора а – единичный вектор, имеющий то же

направление, что и а; обозначается а º.

Отметим важное равенство: a = | a | ∙ a ^°, т.е. любой вектор может быть

представлен в виде произведения его орта на число, равное его модулю, откуда получаем формулу для нахождения орта вектора

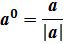
Свойства линейных операций над векторами

Сложение коммутативно: а + b = b + а.

 Сложение ассоциативно: а + (b + с) = (а + b) + с.

 а + 0 = а.

 Дистрибутивность: (λ 1 + λ 2) а = λ 1 а + λ 2 а.

 Дистрибутивность: λ (а + b) = λ а + λ b.

 1 a  a.

 Вектор – а, противоположный вектору а, можно представить в виде:

- a = (-1) ∙ a.

Уравнения прямой.

Общее уравнение прямой. Всякое уравнение первой степени с двумя неизвестными х и у, т.е. уравнение вида

(1)

(где А, В, С – постоянные коэффициенты, причем ) определяет на плоскости прямую. Это уравнение называется общим уравнением прямой.

Частные случаи общего уравнения прямой:

1) если , то уравнение приводится к виду , где 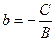(это есть уравнение прямой, параллельной оси Ох);

2) если , то уравнение прямой приводится к виду , где (прямая параллельна оси Оу);

3) если , то уравнение приводится к виду (прямая проходит через начало координат).

2. Уравнение прямой с угловым коэффициентом. Если в общем уравнении прямой , то, разрешив его относительно у, получим уравнение вида

, (2)

где , . Его называют уравнением прямой с угловым коэффициентом.

3. Уравнение прямой в отрезках. Если в общем уравнении прямой , то, разделив все его части на (– С), получим уравнение вида

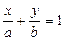, (3)

где , .

4. Уравнение прямой, проходящей через данную точку в данном направлении. Если прямая проходит через точку и ее направление характеризуется угловым коэффициентом k, то уравнение прямой имеет вид

. (4)

5. Данное уравнение (4) с различными значениями коэффициента k называют также уравнениями пучка прямых с центром в точке .

6. Уравнение прямой, проходящей через две точки. Если прямая проходит через точк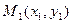и и , то уравнение прямой имеет вид

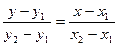, (5)

где , .

7. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору. Если прямая проходит через заданную точку перпендикулярно данному ненулевому вектору , то уравнение прямой имеет вид

. (6)

Вектор , перпендикулярный прямой, называется нормальным вектором этой прямой.

Пример 1. Привести уравнение к нормальному виду.

Решение.

Найдем нормирующий множитель .

Умножая данное уравнение на λ, получим искомое нормальное уравнение прямой: .

10. Угол между прямыми. Если прямые и заданы уравнениями с угловыми коэффициентами и соответственно, то тангенс угла между этими прямыми можно вычислить по формуле

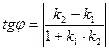. (10)

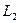11. Условие параллельности двух прямых. Для того чтобы прямые и , заданные уравнениями с угловыми коэффициентами 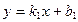и соответственно, были параллельны, необходимо и достаточно, чтобы .

Для того чтобы прямые и , заданные уравнениями и соответственно, были параллельны, необходимо и достаточно, чтобы .

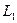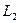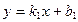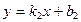12. Условие перпендикулярности двух прямых. Для того чтобы прямые и , заданные уравнениями с угловыми коэффициентами и соответственно, были перпендикулярны, необходимо и достаточно, чтобы .

Для того чтобы прямые и , заданные уравнениями и соответственно, были перпендикулярны, необходимо и достаточно, чтобы .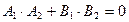

13. Расстояние от точки до прямой. Если прямая задана уравнением и точка не принадлежит данной прямой, то расстояние от точки до прямой находится по формуле