Лекция по «Математическому анализу» 30 марта 2020 года
(Записать в тетрадь конспект лекции)
Применение производной при вычислении пределов
Соотношения вида  и
и  принято относить к разряду неопределенностей при вычислении пределов.
принято относить к разряду неопределенностей при вычислении пределов.
Рассмотрим способ раскрытия неопределенностей  и
и  , который основан на применении производных.
, который основан на применении производных.
Теорема (правило Лопиталя раскрытия неопределенностей вида  ).
).
Пусть функции f (x) и g (x) непрерывны и дифференцируемы в окрестности точки а и обращаются в нуль в этой точке: f (a)= g (a)=0. Пусть  в окрестности точки а. Если существует предел
в окрестности точки а. Если существует предел  , то
, то  .
.
Иначе: предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует.
Пример 1. Найти предел  .
.
Решение: как видно, при попытке непосредственного вычисления предела получается неопределенность вида  . Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
. Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.


 .
.
Пример 2. Найти предел  .
.
Решение: 

 .
.
Теорема (правило Лопиталя раскрытия неопределенностей вида  ).
).
Пусть функции f (x) и g (x) непрерывны и дифференцируемы в окрестности точки а, в этой окрестности  ,
,  . Если существует предел
. Если существует предел  , то
, то  .
.
Пример 3. Найти предел  .
.
Решение:

Замечание. Если при вычислении предела по правилу Лопиталя вновь получается неопределенность  или
или  , то данное правило может быть применено еще раз. Это возможно только в том случае, если вновь полученные функции удовлетворяют требованиям теоремы Лопиталя.
, то данное правило может быть применено еще раз. Это возможно только в том случае, если вновь полученные функции удовлетворяют требованиям теоремы Лопиталя.
Пример 4. Найти предел 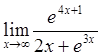 .
.
Решение:


Правило Лопиталя применяется для раскрытия неопределенностей вида  и
и  , которые называются основными. Неопределенности вида
, которые называются основными. Неопределенности вида  ,
,  ,
,  ,
,  сводятся к двум основным видам путем тождественных преобразований.
сводятся к двум основным видам путем тождественных преобразований.
1. Пусть  ,
,  при
при  . Тогда очевидны следующие преобразования:
. Тогда очевидны следующие преобразования:
 или
или  .
.
Пример 5. Вычислить предел  .
.
Решение:

 .
.
2. Пусть или  и
и  , или
, или  и
и 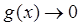 , или
, или  и
и  при
при  . Для нахождения предела вида
. Для нахождения предела вида  удобно сначала прологарифмировать выражение А =
удобно сначала прологарифмировать выражение А =  .
.
Пример 6. Вычислить предел  .
.
Решение: имеем неопределенность вида  . Логарифмируем выражение
. Логарифмируем выражение  , получим:
, получим:  . Затем находим предел:
. Затем находим предел:

 ,
,
т.е.  . Отсюда
. Отсюда  и
и  .
.
Пример 7. Вычислить предел  .
.
Решение: имеем неопределенность вида  . Логарифмируем выражение
. Логарифмируем выражение  , получим:
, получим:  . Затем находим предел:
. Затем находим предел:
 ,
,
т.е.  . Отсюда
. Отсюда  , и
, и  .
.
 2020-04-12
2020-04-12 1082
1082







