2020-04-12
133
Одним из приложений производной является ее применение к исследованию функций и построению графика функции.
Возрастание и убывание функций
Установим необходимые и достаточные условия возрастания и убывания функции, вспомнив предварительно понятие возрастающей и убывающей функции.
Пусть функция 
определена на множестве D и пусть 
– подмножество D.
Определение. Если для любых значений 
аргументов из неравенства 
вытекает неравенство: 
то функция называется возрастающей [неубывающей] на множестве .
Определение. Если для любых значений аргументов из неравенства вытекает неравенство: 
то функция называется убывающей [невозрастающей] на множестве .
Теорема (необходимые условия).
Если дифференцируемая на интервале 
функция 
возрастает (убывает), то 
для любого 
.
Теорема (достаточные условия). Если функция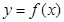 
дифференцируема на интервале и 
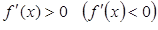для любых , то эта функция возрастает (убывает) на интервале .
Пример. Исследовать функцию 
на возрастание и убывание.
Решение: функция определена на интервале 
.
.
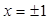– нули производной. Определим знак производной на каждом интервале.
при 
; 
при 
.
Вывод: данная функция возрастает на интервалах 
; убывает на интервале 
.
