2020-04-12
2243
Эвольвентой окружности называется кривая, описываемая точкой прямой линии, перекатываемой по окружности без скольжения.
Рассмотрим построение эвольвенты. На рис. 4 изображена окружность с центром в точке 
. К этой окружности проведена касательная в точке 
. Будем перекатывать прямую по окружности без скольжения. Для этого от точки отложим по прямой ряд одинаковых по длине отрезков 
и т. д. По окружности от точки отложим дуги 
и т.д., равные этим отрезкам.
Рис. 4. Построение эвольвенты Рис. 5. К выводу уравнения
эвольвенты
При перекатывании прямой по окружности без скольжения точка 1 совпадет с точкой 
, точка 2 – с точкой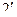 
, точка 3 - с точкой 
и т.д. Проведем в точках 
, 
, ,... касательные к окружности (для точного проведения касательной следует сначала провести радиус и затем к нему провести перпендикуляр) и отложим на них от точек касания отрезки 
, 
, 
,..., равные соответственно отрезкам прямой 
, 
, 
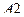,... (или дугам 
, 
, 
, …). Соединяя точки 
, 
, 
,... плавной кривой, получим эвольвенту.
Окружность, по которой перекатывается прямая при образовании эвольвенты, называется основной окружностью. Прямая, перекатываемая по окружности, называется образующей прямой.
Легко видеть, что образующая прямая всегда нормальна к эвольвенте. Действительно, точки касания, образующей прямой с основной окружностью являются при образовании эвольвенты мгновенными центрами вращения образующей прямой, а потому соответствующие отрезки (
, 
, 
,...) являются мгновенными радиусами кривизны эвольвенты. Но радиус кривизны кривой всегда расположен нормально к кривой. Поэтому образующая прямая всегда нормальна к эвольвенте.
Это основное и важнейшее свойство эвольвенты.
Отметим еще некоторые другие свойства эвольвенты.
Эвольвента начинается на основной окружности и всегда расположена вне ее.
Эвольвента является кривой без перегибов.
Форма эвольвенты зависит только от радиуса основной окружности.
Выведем уравнение эвольвенты.
Самостоятельное изучение
Пусть координатами какой-либо точки 
эвольвенты (рис. 5) будут: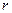 
- радиус-вектор и 
- угол отклонения радиус-вектора от радиуса, проведенного к началу эвольвенты 
(на основной окружности). Проведем из точки касательную к основной окружности радиуса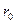 
. Точку касания 
соединим с центром основной окружности 
. Угол между лучами 
и 
обозначим через 
. Из треугольника 
имеем
. (2)
Из свойства эвольвенты следует, что
.
Но
и 
,
тогда
или
.
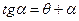Решая относительно 
, получим
. (3)
Выражение 
сокращенно обозначается знаком 
и читается как инволюта :
.
Для инвалютных функций составлены таблицы, по которым по значению угла можно определить значение величины . Учитывая сказанное, угол 
будет равен
. (3а)
Уравнения (2) и (3а) есть уравнения эвольвенты в полярных координатах.
Эвольвентное зацепление.
Пусть вращательное движение передается при помощи двух кулачков, профили которых выполнены по кривым 
и 
, являющимися эвольвентами основных окружностей радиусов 
и 
(рис. 6).
Рис. 6. Эвольвентное зацепление
На основании основной теоремы зацепления и основного свойства эвольвенты легко показать, что передаточное отношение этой передачи постоянно. Действительно, общая касательная 
к основным окружностям нормальна к каждой из эвольвент (на основании основного свойства эвольвенты) и поэтому проходит всегда через точку их касания. Прямая , являясь общей нормалью в точке касания к обеим поверхностям, делит межосевое расстояние 
на отрезки, обратно пропорциональные угловым скоростям (на основании основной теоремы зацепления):
.
Так как прямая 
всегда касается одних и тех же окружностей, то занимает всегда одно и то же положение, т.е. пересекает межосевое расстояние в постоянной точке 
. Следовательно, передаточное отношение 
постоянно.
Геометрическое место точек касания профилей (зубьев) называется линией зацепления.
В эвольвентном зацеплении линией зацепления является прямая - касательная к основным окружностям, так как эвольвенты касаются только на этой прямой.
В этом заключается одно из достоинств эвольвентного зацепления. Действительно, зуб одного колеса давит на зуб другого колеса, если пренебречь трением, всегда по линии . Поэтому направление силы не изменяется, что благоприятно сказывается на прочности конструкции зубчатого механизма.
Угол 
отклонения линии зацепления от общей касательной к начальным окружностям в точке называется углом зацепления. Для нормального зубчатого зацепления этот угол равен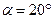 
.
Необходимо отметить, что если несколько увеличить межосевое расстояние , то передаточное отношение не изменится. В самом деле, из подобия треугольников 
и 
следует
,
тогда
, (4)
т.е. передаточное отношение обратно пропорционально радиусам основных окружностей. Так как эти радиусы являются постоянными для данных кулачков, то при изменении межосевого расстояния передаточное отношение не изменится. Несколько изменится лишь положение линии зацепления, т. е. угол зацепления .
Постоянство передаточного отношения при изменении межосевого расстояния – является положительным качеством эвольвентной зубчатой передачи, так как неизбежные погрешности при сборке зубчатых механизмов не будут оказывать влияния на передаточное отношение.
Основные геометрические параметры нормальных зубчатых колес.
На рис. 7 представлено сечение зубчатого колеса плоскостью, перпендикулярной оси колеса. Как видно из этого рисунка, начальная окружность делит зуб по высоте на две части: на головку зуба высотой 
и ножку зуба высотой 
.
Зуб имеет два профиля: левый (
) и правый (
), очерченные по эвольвентным кривым.
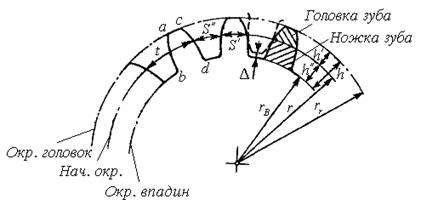
Рис. 7. Основные геометрические параметры стандартного зубчатого зацепления
Расстояние между одноименными точками двух соседних зубьев, измеренное по начальной окружности, называется шагом зубчатого колеса. Шаг 
складывается из двух частей: толщины зуба 
и ширины впадины между зубьями 
, измеряемыми также по начальной окружности:
. (5)
Для нормальных зубчатых колес принято, что толщина зуба и ширина впадины по начальным окружностям должны быть одинаковы:
. (6)
Шаг обоих зубчатых колес, находящихся в зацеплении, по начальным окружностям должен быть одинаков (так как начальные окружности катятся одна по другой без скольжения).
Длина начальной окружности колеса равна
, (7)
где 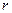- радиус начальной окружности;
- количество зубьев зубчатого колеса.
Из уравнения (7) следует, что диаметр начальной окружности зубчатого колеса равен
. (7а)
Отсюда видно, что диаметр 
и шаг выражаются несоизмеримыми числами, так как в правую часть входит трансцендентное число 
. Для облегчения расчетов, измерения и изготовления зубчатых колес отношение 
стандартизовано и выражается целыми числами или числами с простой десятичной дробью. Это отношение шага зубчатого зацепления к числу 
называется модулем зубчатого зацепления и обозначается буквой 
:
. (8)
Модуль выражается в миллиметрах и выбирается в соответствии с ГОСТ 9563-61.
Диаметр начальной окружности колеса, как это следует из уравнения (7а) и (8), равен
(7б)
Шаг зубчатого колеса
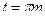. (8а)
Толщина зуба и ширина впадины по начальной окружности
(6а)
Для нормального зубчатого колеса принято, что высота головки зуба равна
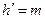, (9)
а высота ножки зуба
. (10)
Высота головки зуба 
делается несколько меньше высоты ножки зуба 
, для того чтобы вершина зуба одного колеса не упиралась в основание впадины другого колеса, т.е. чтобы обеспечить радиальный зазор, который равен (см. рис. 7)
. (11)
Диаметр окружности головки зубчатого колеса (см. рис. 5)
или
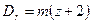. (12)
Диаметр окружности впадины зубчатого колеса
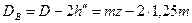
или
. (13)
Пользуясь формулой (12), на практике легко определить модуль зубчатого колеса, для чего достаточно измерить диаметр окружности головок и подсчитать количество зубьев:
.
Из равенства (7б) следует
,
т.е. модуль выражается отношением диаметра начальной окружности к количеству зубьев колеса. Поэтому модуль иногда называют диаметральным шагом.
Расстояние между осями двух колес, находящихся в зацеплении, равно сумме радиусов начальных окружностей
или
, (14)
т.е. межосевое расстояние равно половине произведения модуля зацепления на сумму зубьев зубчатых колес.
Это свойство часто используется в технике. Например, в токарных станках для изменения передаточного отношения применяются сменные шестерни, которые устанавливаются между валами, межосевое расстояние которых постоянно. При этом требуется, чтобы сохранилась сумма зубьев устанавливаемой пары шестерен (модуль всех колес одинаков).
Как видно из приведенных формул, все размеры зубчатого колеса и зуба – диаметры начальной окружности, окружностей головок и впадин, высота зуба, толщина зуба, шаг и др. – выражаются в долях модуля. Чем больше модуль, тем больше размеры колеса и размеры зуба и, следовательно, тем зуб прочнее. Величина модуля определяется в курсе деталей машин из условия расчета зуба на прочность.
Передаточное отношение зубчатой передачи может быть выражено через количество зубьев колес
.
Отметим, что эта формула справедлива лишь для одной пары зубчатых колес. Метод определения передаточного отношения через количество зубьев для сложных зубчатых механизмов, состоящих из многих колес, будет рассмотрен далее.
