Основная теорема зацепления

Передача движения в зубчатых колесах происходит нажатием зуба одного колеса на зуб другого колеса. Какими же должны быть профили зубьев колес, чтобы передаточное отношение было строго постоянным, т.е. чтобы начальные окружности перекатывались друг по другу без скольжения?

Ответ на этот вопрос даст нам основная теорема зацепления, которая формулируется следующим образом: общая нормаль в точке касания звеньев высшей кинематической пары делит межосевое расстояние на отрезки, обратно пропорциональные угловым скоростям.

Докажем эту теорему.

На рис. 1 изображены два звена, которые, касаясь в точке , образуют высшую кинематическую пару (это могут быть зубья двух зубчатых колес). Звено 1, вращаясь вокруг оси  с угловой скоростью , воздействует на звено 2, заставляя его вращаться вокруг оси  с угловой скоростью . Проведем через точку касания  общие касательную  и нормаль .

                          Рис. 1. К основной теореме зацепления

 

Оба звена должны быть в постоянном соприкосновении. Для этого необходимо, чтобы проекции скоростей точки касания  обоих звеньев на общую нормаль были равны. В противном случае либо одно звено опередит другое (нарушится контакт), либо одно звено врежется в другое.

Проведем векторы скоростей точки  обоих звеньев. Вектор  скорости точки  звена 1 перпендикулярен радиус-вектору , вектор  скорости точки  звена 2 перпендикулярен радиус-вектору . Разложим каждый из этих векторов на две составляющие - нормальные  и 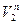 и касательные -  и . Нормальные составляющие, как уже указывалось, должны быть равны

.

Но

 и ,

где  и 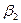 - углы отклонения соответственно векторов  и  от нормали .

Следовательно,

.

Учитывая, что  и , получим

.

Восстановим из точек 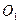 и  перпендикуляры на нормаль  и . Величины этих перпендикуляров равны:

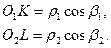
Тогда

,

откуда

.

Треугольник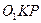и  и  подобны, следовательно,

.

Сопоставляя последние два равенства, окончательно получим

                                                          .                                                    (1)

Теорема доказана.

Из равенства (1) следует: чтобы передаточное отношение было постоянным, необходимо, чтобы отрезки  и , на которые нормаль  делит межосевое расстояние, были постоянной величины. Другими словами, необходимо, чтобы нормаль всегда, в любом положении звеньев, проходила через одну и ту же точку .

Все кривые, удовлетворяющие этому условию, могут быть использованы для образования боковых поверхностей зубьев цилиндрических колес. Такие кривые называются сопряженными. Задаваясь произвольно профилем зуба одного колеса, можно построить сопряженный профиль зуба другого колеса. Таких кривых может быть теоретически бесконечное количество. Однако на практике в подавляющем большинстве случаев пользуются эвольвентным зацеплением, в котором боковые профили зубьев колес выполнены, по эвольвентным кривым.

Точка  пересечения нормали  с линией центров является полюсом зацепления. Она является мгновенным центром вращения звеньев в относительном движении. В самом деле, из равенства (1) видно, что скорости точки , принадлежащей обоим колёсам, равны

.

При постоянном передаточном отношении  отрезки  и  являются радиусами начальных окружностей.

Из рис. 1 видно, что касательные составляющие скоростей точек касания  и  не равны между собой, следовательно, профили зубьев скользят друг по другу. Это вызывает износ зубьев. Только в одном положении, когда точка касания зубьев совпадает с полюсом зацепления 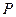, нет скольжения между профилями зубьев, так как скорости точек касания в этом положении векторно равны. Скольжение между зубьями будет тем больше, чем дальше находится точка касания от полюса зацепления.

 

Рассмотрим несколько примеров, основанных на теореме зацепления (самостоятельное изучение).

  

Пример 1. Определить отношение угловых скоростей звеньев 1 и 2 трехзвенного механизма с одной высшей кинематической парой для положений, при которых углы между ведущим звеном 1 и линией центров  равны  и .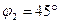

Дано: межосевое расстояние .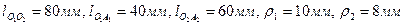

 Решение. 1. Строим положение механизма, соответствующее углу  (рис. 2, а). Для этого из центра  под углом  к линии центров откладываем в масштабе отрезок  и из точки  проводим окружность радиусом . Далее из точки  радиусом  проводим дугу, а из точки  на этой дуге делаем засечку радиусом . Полученная точка есть точка . Проводим из этой точки окружность радиусом  - профиль второго звена высшей кинематической пары.

Аналогично строим положение механизма для угла  (рис. 2, б).

2. Через точку  касания звеньев высшей кинематической пары проводим общую нормаль  (она проходит через центры кривизны  и ) до пересечения с линией центров 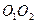 в точке .

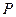3. Измеряем отрезки  и  для обоих случаев:

для

для

Тогда в соответствии с теоремой зацепления имеем:

для

для

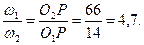
Как видно, отношение угловых скоростей в разных положениях механизма различно.Это естественно, так как профили звеньев 1 и 2 выбраны произвольно.   

        Рис. 2. К примеру 1                                                    Рис. 3. К примеру 2  

 

Пример 2. Определить отношение угловых скоростей звеньев 1 и 2 механизма, представленного на рис. 3, для положений, при которых ведущее звено 1 составляет с линией центров 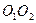 углы  и .

 Дано: межосевое расстояние , длина звена 1 .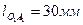

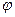Решение. 1. Строим заданные положения механизмов. Для этого к линии центров  под заданным углом  от точки  откладываем отрезок , изображающий в масштабе звено 1. Тогда звено 2 займет положение , проходящее через точки  и  (положения механизмов для углов  и 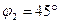 показаны соответственно на рис. 3, а, б).                        

2. Измеряем отрезки  и  для обоих случаев:

для

для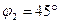

Тогда в соответствии с основной теоремой зацепления имеем:

для

для

Как видно, отношение угловых скоростей звеньев в разных положениях механизма различно.