2020-04-12
142
Формулы основаны на законах Кирхгофа. Метод можно применить для расчета схемы, имеющей 2 узла.
В
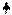I 1 I 2 I 3 I
Е 1 Е 2 Е 3
R
 | |||||||
 | |||||||
 | | ||||||
R 01 R 02 R 03
 | |||||
 | |||||
 | |||||
A
Токи надо направить во всех ветвях в одну сторону, например, от узла А к узлу В.
Находим проводимости всех ветвей
; 
; 
; 
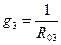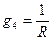
Находим узловое напряжение
Узловое напряжение равно алгебраической сумме произведений ЭДС и проводимостей ветвей, деленной на сумму проводимостей всех ветвей.
ЭДС входит в формулу со знаком «+», если ее направление совпадает с направлением тока, в противном случае ей присваивают знак «–».
Определяем токи ветвей по формулам:
I 1 = (Е 1 – U AB) g 1
I 2 = (Е 2 – U AB) g 2
I 3 = (Е 3 – U AB) g 3
I = – U AB· g
Решим задачу в общем виде, применяя метод узлового напряжения
 R 3
         I 1 I 2 I 3
Е 1 Е 2 Е 4
R 01 R 04
     Е 3
R 03 R 4
R 1 R 2
  R 5
|
|
Проводимость ветви – величина, обратная ее эквивалентному сопротивлению.
I 1 = (Е 1 – U AB)· g 1
I 2 = (Е 2 – Е 3 – U AB)· g 2
I 3 = (– Е 4 – U AB)· g 4
Графоаналитический метод расчета нелинейных цепей
Постоянного тока
Нелинейной называется электрическая цепь, которая содержит хотя бы один нелинейный элемент.
Сопротивление нелинейного элемента не является величиной постоянной и зависит от различных факторов: температуры, давления, величины и полярности напряжения и т.д.
Условное обозначение
|
Для расчета цепей с нелинейными элементами необходимо знать его вольтамперную характеристику (ВАХ).
  I
  1
2
 U
|  I
  U
|
| (1) ВАХ лампы накаливания с вольфрамовой нитью; (2) ВАХ линейного элемента (R = const). | ВАХ полупроводникового диода. |
Рассмотрим последовательное соединение нелинейных элементов.
R1 R2
○ ○ ВАХ R1 и R2 известны.
Для решения любой задачи надо построить обобщенную ВАХ всей цепи. При построении необходимо учесть, что для любого значения тока напряжение на зажимах цепи определяется суммой напряжений на отдельных элементах.
  1 2 3
 I
      
 
  
    
   U
  
   = +
|
При токе 
при токе 
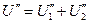и т.д.
|
1 – ВАХR1
2 – ВАХR2
3 – ВАХ последовательного соединения R1 и R2.
Рассмотрим параллельное соединение.
I
     ○
  I 1 I 2
  U R 1 R 2
○
| При параллельном соединении при любом значении напряжения общий ток равен сумме токов ветвей. |
 I
ВАХ параллельного
  соединения
   
   ВАХR2
      
    ВАХR1
   
|
При напряжении 
при напряжении 
и т.д.
Обобщенная ВАХ позволит ответить на любой вопрос задачи
|
Рассмотрим последовательное соединение линейного и нелинейного элементов.
R1 R2
○ ○ Дано: U; R 1, задана ВАХR2
U
Определить: I; U R1; U R2
 I
    ВАХR2
  I A
U R2 U R1 U
| Уравнение прямой нагрузки
U = U R1 + U R2
U = I R1 + U R2
 
|
U
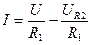
Решение задачи должно удовлетворить прямой нагрузки, а также ВАХR2
Построим прямую нагрузки по 2-м точкам:
U R2 = 0 → 
U R2 = U → I = 0
Решение задачи – точка пересечения графиков А.
Ордината (.) А – искомый ток I.
Абсцисса (.) А – напряжение на нелинейном элементе U R2.
Напряжение на линейном элементе
U R1 = U – U R2
