· Операция сложения.
Суммой двух свободных векторов  и
и 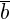 называется свободный вектор
называется свободный вектор 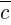 , начало которого совпадает с началом первого, а конец — с концом второго, если совмещены конец вектора
, начало которого совпадает с началом первого, а конец — с концом второго, если совмещены конец вектора  и начало вектора
и начало вектора 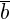 .
.
Сумма двух векторов  и
и 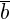 (
(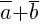 ) — это вектор, идущий из начала вектора
) — это вектор, идущий из начала вектора  в конец вектора
в конец вектора 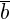 при условии, что начало вектора
при условии, что начало вектора 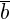 приложено к концу вектора
приложено к концу вектора  (правило треугольника).
(правило треугольника).
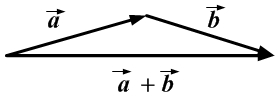
Свойства операции сложения векторов:
1) Переместительное свойство: 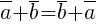 (коммутативность).
(коммутативность).
2) Сочетательное свойство: 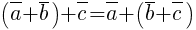 (ассоциативность).
(ассоциативность).
3) Существует нулевой вектор 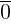 , такой, что
, такой, что 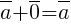 для любого вектора
для любого вектора  (особая роль нулевого вектора).
(особая роль нулевого вектора).
Нулевой вектор 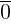 порождается нулевым закрепленным вектором, то есть точкой.
порождается нулевым закрепленным вектором, то есть точкой.
4) Для каждого вектора  существует противоположный ему вектор
существует противоположный ему вектор 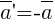 , такой, что
, такой, что 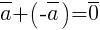 . Вектор
. Вектор 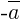 называется вектором, противоположным вектору
называется вектором, противоположным вектору  .
.
Правило параллелограмма (правило сложения векторов): если векторы  и
и 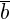 приложены к общему началу и на них построен параллелограмм, то сумма
приложены к общему началу и на них построен параллелограмм, то сумма 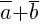 этих векторов представляет собой диагональ параллелограмма, идущую из общего начала векторов
этих векторов представляет собой диагональ параллелограмма, идущую из общего начала векторов  и
и 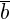
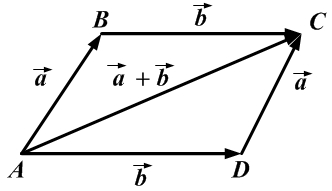
Вычитание векторов определяется через сложение: 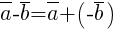 .
.
Другими словами, если векторы  и
и 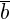 приложены к общему началу, то разностью векторов
приложены к общему началу, то разностью векторов  и
и 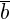 будет вектор
будет вектор 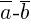 , идущий из конца вектора
, идущий из конца вектора 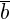 к концу вектора
к концу вектора  .
.
· Операция умножения вектора на число.
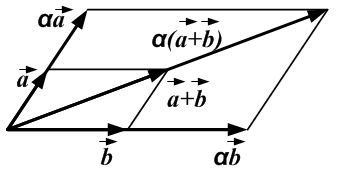
Произведением вектора  на число
на число 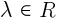 называется вектор
называется вектор 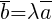 такой, что:
такой, что:
1) если λ > 0,  ≠
≠ 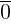 , то
, то 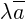 получается из
получается из  растяжением в λ раз:
растяжением в λ раз: 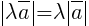 ;
;
2) если λ < 0,  ≠
≠ 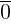 , то
, то 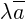 получается из
получается из  растяжением в | λ | раз и последующим отражением:
растяжением в | λ | раз и последующим отражением: 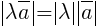 ;
;
3) если λ = 0 или 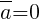 , то
, то 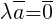 .
.
Свойства операции умножения:
1) Распределительное свойство относительно суммы чисел: 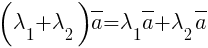 для любых действительных
для любых действительных 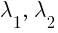 и всех
и всех  (дистрибутивность).
(дистрибутивность).
2) Распределительное свойство относительно суммы векторов: 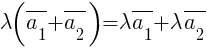 (дистрибутивность).
(дистрибутивность).
3) Сочетательное свойство числовых сомножителей: 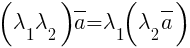 (ассоциативность).
(ассоциативность).
4) Существование единицы: 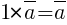 .
.
 2020-04-12
2020-04-12 165
165








