Ортонормированный базис (ОНБ) — это три взаимно перпендикулярных вектора с длинами, равными единице.

Обозначения: 
· Базисные орты — это векторы  .
.
· Зафиксированная точка О – это начало координат.
Отложим от точки O векторы  .
.
Полученная система координат — это прямоугольная декартова система координат.
· Декартовы координаты вектора — это координаты любого вектора в этом базисе:

Пример 11.
· Координатные оси — это прямые линии, проведенные через начало координат (точку O) по направлениям базисных векторов:
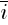 – порождает Ox;
– порождает Ox;
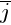 – порождает Oy;
– порождает Oy;
 – порождает Oz.
– порождает Oz.
· Абсцисса — это координата точки M (вектора  в декартовой системе координат по оси Ox.
в декартовой системе координат по оси Ox.
Ордината — это координата точки M (вектора  в декартовой системе координат по оси Oy.
в декартовой системе координат по оси Oy.
Аппликата — это координата точки M (вектора  ) в декартовой системе координат по оси Oz.
) в декартовой системе координат по оси Oz.
· Декартовы прямоугольные координаты x, y, z вектора  равны проекциям этого вектора на оси Ox, Oy, Oz, соответственно. Иначе:
равны проекциям этого вектора на оси Ox, Oy, Oz, соответственно. Иначе:

где α, β, γ – углы, которые составляет вектор  с координатными осями Ox, Oy, Oz, соответственно, при этом cosα, cosβ, cosγ называются направляющими косинусами вектора
с координатными осями Ox, Oy, Oz, соответственно, при этом cosα, cosβ, cosγ называются направляющими косинусами вектора 
Для направляющих косинусов справедливо соотношение:

· Орт направления — это вектор  единичной длины данного направления.
единичной длины данного направления.
Скалярное произведение векторов  .
.
· Скалярное произведение двух векторов  — это число
— это число  где
где 
· Выражение скалярного произведения в декартовых координатах:
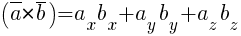
· Алгебраические свойства скалярного произведения:
1)  ;
;
2)  ;
;
3)  ;
;
4)  — не нулевой вектор и
— не нулевой вектор и  , если
, если  — нулевой вектор.
— нулевой вектор.
· Длина вектора  :
:
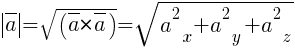
Пример 13.
· Косинус угла между векторами:

· Проекция вектора  на вектор
на вектор 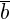 :
:

· Условие перпендикулярности ненулевых векторов  и
и 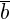 :
:

· Векторное произведение векторов 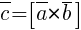 :
:
1) модуль  где
где 
2) 
3) тройка векторов  — правая.
— правая.
· Алгебраические свойства векторного произведения:
1) 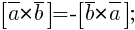
2) 
3) 
4) 
· Выражение векторного произведения в декартовых координатах:

· Геометрические свойства векторного произведения:
1) Площадь параллелограмма, построенного на векторах  и
и 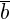 равна:
равна:

2) Условие коллинеарности ненулевых векторов  и
и 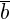 :
:

· Двойное векторное произведение векторов:
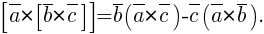
· Смешанное произведение векторов:

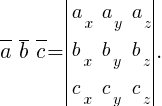
· Объем параллелепипеда:
 Пример 14.
Пример 14.
· Объем пирамиды:
 Пример 15.
Пример 15.
· Условие компланарности 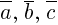 :
:

 2020-04-12
2020-04-12 738
738







