Разложение вектора по базису

· Базис и координаты.
Базис в пространстве — это три некомпланарных вектора, взятые в определенном порядке.
Базис на плоскости — это два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.
Базис на прямой — это любой ненулевой вектор этой прямой.

· Теорема 1. Каждый вектор может быть разложен по базису в пространстве и это разложение единственно.

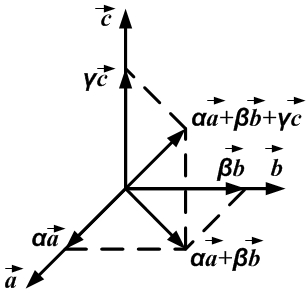
Другими словами, если 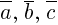— три некомпланарных вектора в пространстве, то любой вектор 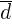может быть записан в виде: .
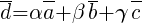Коэффициенты разложения вектора по базису — это координаты вектора в данном базисе, и в каждом базисе определяются однозначно:
.
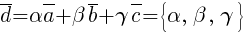Теорема2. При сложении двух векторов 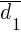и 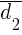их координаты (относительно любого базиса) складываются. При умножении вектора 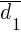на любое число 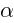все его координаты умножаются на это число.
Система координат в пространстве — это совокупность базиса 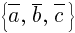и некоторой точки, называемой началом координат.
Радиус-вектор точки M — это вектор , идущий из начала координат в точку M.
Координаты точки 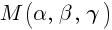— это координаты вектора .
Таким образом, координаты радиус-вектора и координаты точки M совпадают.