Процентные облигации и векселя

 

Пусть бумага данного вида эмиттирована в момент времени T_I по цене N₀, причем эта цена может быть как выше, так и ниже номинала (это обусловлено соотношением объявленной купонной ставки и среднерыночной ставки заимствования, с учетом периодичности платежей). Обозначим размер купона DN, а число равномерных купонных выплат длительностью Dt за период обращения обозначим за K, причем для общности установим, что платеж по последнему купону совпадает с моментом погашения бумаги.

 

Тогда временная последовательность купонных платежей может быть отображена вектором на оси времени с координатами

 

                                    (6.22)

 

Формула для справедливой цены процентного долгового инструмента имеет вид:

 

                                                           (6.23)

 

где

 

 -                                                     (6.24)

 

номер интервала, которому принадлежит рассматриваемый момент t,

 

                                      (6.25)

 

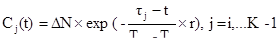,                                  (6.26)

 

моменты t_i определяются соотношением (6.22), а внутренняя норма доходности долгового инструмента r отыскивается как корень трансцендентного уравнения вида

 

С(T_I) = N₀.                                                                          (6.27)

 

Если купон по процентной бумаге нулевой, то переходим к рассмотренному выше случаю дисконтной бумаги.

 

Анализ соотношений (6.25) и (6.26) показывает, что шум цены, тренд которой имеет вид (6.23), является нелинейно затухающей кусочной функцией на каждом интервале накопления купонного дохода, причем шум получает как бы две составляющих: глобальную – для всего периода обращения бумаги, и локальную – на соответствующем моменту t интервале накопления купонного дохода.

 

Исследуем характер шума цены процентной бумаги:

 

                                                                     (6.28)

 

где C(t) – тренд цены - определяется по (6.23).

 

Руководствуясь соображениями, изложенными в предыдущем примере дисконтных бумаг, будем отыскивать СКО шума цены в виде:

 

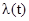                                                                      (6.29)

 

 где

 

                                        

(6.30)

 

а i определяется по (6.24). Соотношение (6.30) является частной производной справедливой цены (6.23) по показателю внутренней нормы доходности бумаги с точностью до постоянного множителя.

 

Аналогично предыдущему примеру, мы можем получить нормировочный делитель для шума цены процентной бумаги. Переход от нестационарного шума к стационарному будет иметь вид:

 

,                                                                     (6.31)

 

где 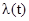определяется по (6.30). При уменьшении величины купона до нуля соотношение (6.29) переходит в (6.9), что косвенно подтверждает правоту наших выкладок.

 

На рис. 6.3 приведен примерный вид тренда цены процентной бумаги, а на рис. 6.4 – примерный вид СКО такой бумаги.

 

Рис. 6.3. Функция справедливой цены процентной бумаги

 

Рис. 6.4. Функция СКО процентной бумаги

Что касается доходности процентных инструментов, то формулы (6.12) – (6.13) получают поправку в виде проплаченного за время Т купонного дохода:

 

(6.32)

 

где m – число оплаченных купонов процентной бумаги за период T.

 

Вывод о том, что случайный процесс 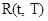имеет в своем сечении нормальную величину, сохраняется без изменений. Параметры этой случайной величины:

 

                                  (6.33)

 

                                                            (6.34)

 

Рассмотрим расчетный пример.

Расчетный пример 6.2

Облигация номиналом N = 1000$ выпускается в обращение в момент времени T_I = 0 (далее все измерения времени идут в годах) сроком на 3 года c дисконтом 10%, то есть по эмиссионной цене N₀ = 900$. По бумаге объявлено три годовых купона по ставке 20% годовых, то есть размером DN = 200$. Инвестор намеревается приобрести бумагу в момент времени t =1 сразу после первого купонного платежа. В этот момент текущая цена бумаги на рынке составляет H(1) = 940$. Для проведения статистического анализа доступна история сделок с бумагой за истекший год ее обращения. Требуется идентифицировать доходность облигации R(t=1, T) на протяжении оставшихся двух лет владения (T Î [0, 2]) как случайный процесс и определить параметры этого процесса.

Решение

Определим внутреннюю норму доходности нашей процентной бумаги, итеративно решив уравнение (6.27). Тогда, согласно (6.23), это уравнение приобретает вид:

(1000 + 200) * exp(-r) + 200*(exp(-r/3) + exp(-2r/3)) = 900,      (6.35)

 

откуда методом итераций получаем r = 67.2% годовых.

 

Выражение для справедливой цены приобретает вид:

 

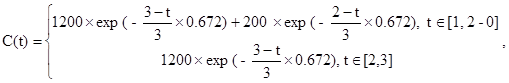(6.36)

Далее следует этап анализа истории цены за истекший год. СКО шума цены, согласно (6.29) – (6.30), имеет вид

 

                                                                       (6.37)

 

где

 

(6.38)

 

а s₀ определяется на основе анализа истории скорректированного шума цены вида (6.31).

 

Теперь бумага полностью идентифицирована. Случайный процесс ее доходности имеет параметры, которые определяются по формулам (6.13), (6.14). В частности, на момент погашения бумаги Т = 2, C(3) = 1200$, s(1+2) = 0, e(1+2) = 0, и R(1,2) = (1200-940)/(940*2) = 13.83% годовых – неслучайная величина.

 

Оценим процесс количественно через Т = 1 год владения бумагой непосредственно перед получением дохода по второму купону, задавшись параметром СКО шума s₀ = 20$. Тогда

 

C(2-0) = 1200*exp(-(3-2)*0.672/3) + 200 = 1159.2$,        (6.39)

 

,                  (6.40)

 

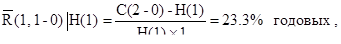                       (6.41)

                                  (6.42) 

 

 Нечетко-множественный подход

 

Обладая квазистатистикой ценового поведения облигации, мы можем оценить СКО шума цены (6.9) и (6.29) как треугольную нечеткую функцию фактора времени, по аналогии с тем, как это делается в главе 5 книги. И все соответствующие вероятностные распределения приобретают вид нечетких функций, а случайные процессы приобретают постоянные нечеткие параметры.

 

 

Выводы

 

     Мы получили вероятностную интерпретацию цены долгового инструмента. Это новый подход к анализу бумаг такого рода, но он обещает быть весьма плодотворным, когда дело дойдет до оптимизации смешанных портфелей, содержащих как акции или паи, так и долговые обязательства. Зная матожидание и дисперсию цены, мы можем оценивать то же для текущей доходности. И тогда мы можем решать задачу Марковица, отыскивая максимум доходности портфеля при фиксированном СКО портфеля. Подробно это обсуждается в главе 8 настоящей монографии.

 

     Если квазистатистики по отдельной долговой бумаге нет, можно воспользоваться статистикой квазистатистикой ведущих индексов по долговым обязательствам (например, индексами доходности по 10-летним или 30-летним государственным долговым обязательствам, анализируемыми в пределах последнего года). Параметры случайных процессов для этих индексов могут быть взяты за основу при моделировании ценовых случайных процессов для индивидуальных долговых обязательств, при этом мера уверенности эксперта в оценке параметров будет находиться в обратной зависимости от ширины расчетного коридора, формируемого соответствующими нечеткими числами и вероятностными распределениями с нечеткими параметрами.