Пусть f(t) и g(t) - интегрируемые на любом конечном интервале функции. Свертка функций f(t) и g(t) определяется соотношением

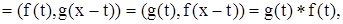
если только интеграл существует и интегрируем по любому конечному интервалу переменной х. Равенство двух интегралов легко проверить, сделав замену z = x-t.
Если f(t), g(t) – регулярные обобщенные функции и j(х) Î K, то можно записать
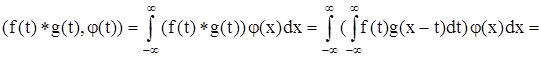
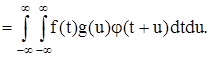
Произведение f(t) g(u) можно рассматривать как прямое произведение f(t) х g(u), так что

Это соотношение определяет свертку обощенных функций f(t), g(t) Î K', включая и сингулярные обобщенные функции.
Свертка обобщенных функций обладает следующими свойствами:
1) 
2) 
3) 
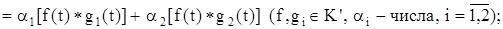
4) если  то
то
 (3)
(3)
Приведем доказательство последнего соотношения. Действительно, для j(х) Î K
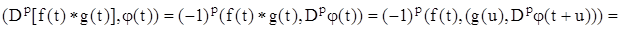

или



что и доказывает соотношение (3).
Примеры:
1. 
2. 
Преобразование Фурье обобщенных функций
Пусть основное пространство K состоит из бесконечно дифференцируемых комплексно-значных функций j(t) действительного переменного t, равных нулю вне некоторого конечного интервала. Преобразование Фурье функции j(t) определяется соотношением

Если рассматривать s как комплексную переменную s = u + iv, то

и y(t) – бесконечно дифференцируемая функция (аналитическая) во всей комплексной плоскости. Интегрируя по частям, получаем
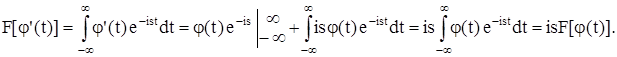
В общем случае можно записать

Далее, если  - дифференциальный полином с постоянныим коэффициентами
- дифференциальный полином с постоянныим коэффициентами  то
то

Определение. Преобразование Фурье обобщенной функции f(t) называется обобщенная функция F[f(t)] = F(s), определяемая соотношением
(F[f(t)], F[j(t)]) = 2p(f(t), j(t)),
которое для регулярных функций называется равенством Парсеваля.
Свойства преобразования Фурье
1) 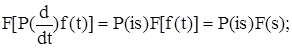
2) 
3) F-1[F[f(t)]] = f(t), где F-1 – оператор, обратный F, удовлетворяющий соотношению 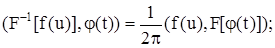
4) F[F[f(t)]] = 2pf(-t);
5) 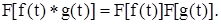
Приведем преобразование Фурье от некоторых обобщенных функций.
F[1(t)] = 2pd(u),
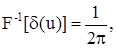
F[d(t-a)] = e-iua,
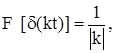

 2020-04-20
2020-04-20 277
277








