Преобразование Лапласа обобщенных функций

 

Определение. Комплекснозначная функция f(t) действительного переменного t называется оригиналом, если

1) f(t) = 0 для t < 0;

2) f(t) – кусочно дифференцируема;

3)

Тогда функция 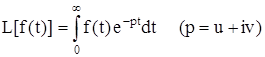 называется преобразованием Лапласа функции f(t). Функция L(p) бесконечно дифференцируема в полуплоскости Re p > a и для нее справедливо соотношение

 

Если то

 

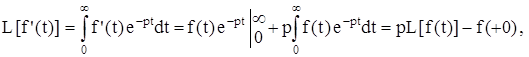
где f(+0) – скачок функции f(t) в начале координат. Обратное преобразование Лапласа L^-1 равно

 

 

Приведем преобразование Лапласа некоторых функций:

 

 

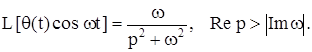
Определение. Преобразование Лапласа обобщенной функции f(t) определяется соотношением

Свойства.

 

1)

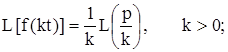
2)

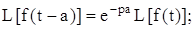
3)

 

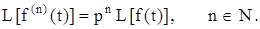
Здесь производные нужно рассматривать как производные обобщенных функций.

Заметим, что

 

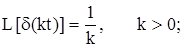
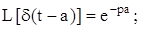
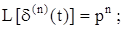
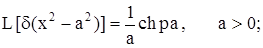
4)

 

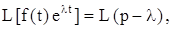
тогда

 

 

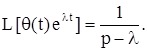
5) Найдем преобразование Лапласа свертки обобщенных функций f(t) и g(t):

 

 

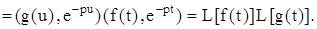
Cледовательно

 

 

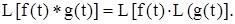
Так как 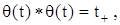 то

 

 

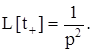
Аналогично можно написать

 

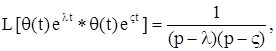
Приведем преобразование Лапласа часто используемых обобщенных функций:

 

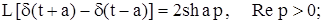
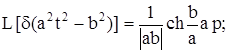
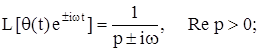
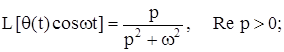
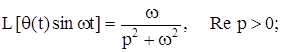
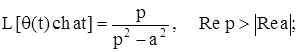
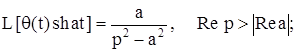
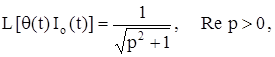
где I_o - функция Бесселя нулевого порядка.